Mitigating large adversarial perturbations on X-MAS (X minus Moving Averaged Samples)
Paper and Code
Jan 23, 2020
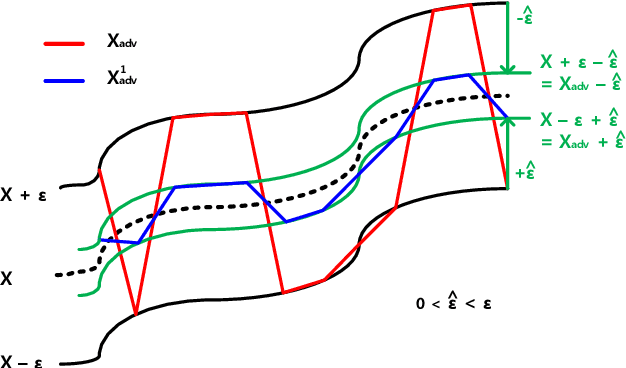

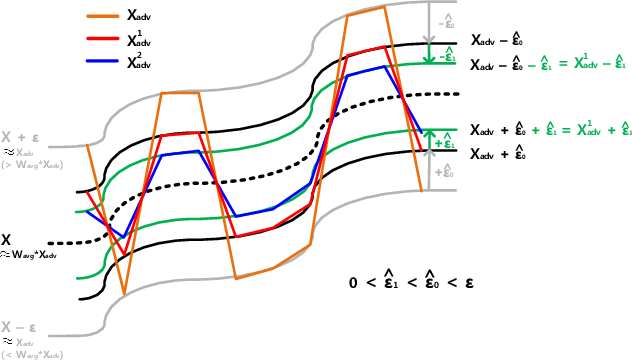
We propose the scheme that mitigates the adversarial perturbation $\epsilon$ on the adversarial example $X_{adv}$ ($=$ $X$ $\pm$ $\epsilon$, $X$ is a benign sample) by subtracting the estimated perturbation $\hat{\epsilon}$ from $X$ $+$ $\epsilon$ and adding $\hat{\epsilon}$ to $X$ $-$ $\epsilon$. The estimated perturbation $\hat{\epsilon}$ comes from the difference between $X_{adv}$ and its moving-averaged outcome $W_{avg}*X_{adv}$ where $W_{avg}$ is $N \times N$ moving average kernel that all the coefficients are one. Usually, the adjacent samples of an image are close to each other such that we can let $X$ $\approx$ $W_{avg}*X$ (naming this relation after X-MAS[X minus Moving Averaged Samples]). By doing that, we can make the estimated perturbation $\hat{\epsilon}$ falls within the range of $\epsilon$. The scheme is also extended to do the multi-level mitigation by configuring the mitigated adversarial example $X_{adv}$ $\pm$ $\hat{\epsilon}$ as a new adversarial example to be mitigated. The multi-level mitigation gets $X_{adv}$ closer to $X$ with a smaller (i.e. mitigated) perturbation than original unmitigated perturbation by setting the moving averaged adversarial sample $W_{avg} * X_{adv}$ (which has the smaller perturbation than $X_{adv}$ if $X$ $\approx$ $W_{avg}*X$) as the boundary condition that the multi-level mitigation cannot cross over (i.e. decreasing $\epsilon$ cannot go below and increasing $\epsilon$ cannot go beyond). With the multi-level mitigation, we can get high prediction accuracies even in the adversarial example having a large perturbation (i.e. $\epsilon$ $>$ $16$). The proposed scheme is evaluated with adversarial examples crafted by the FGSM (Fast Gradient Sign Method) based attacks on ResNet-50 trained with ImageNet dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge