Minimum Volume Topic Modeling
Paper and Code
Apr 03, 2019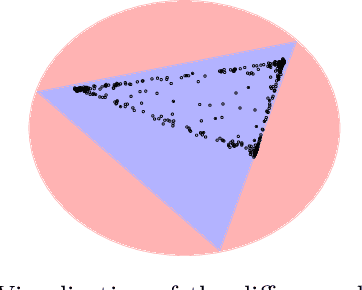
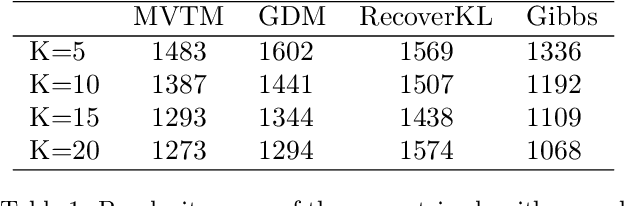
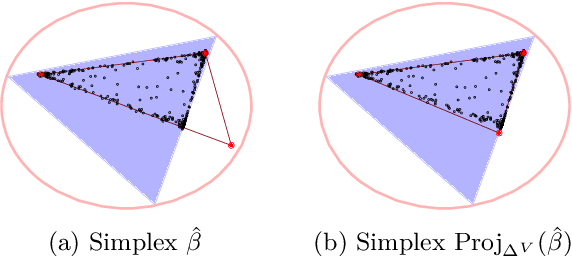
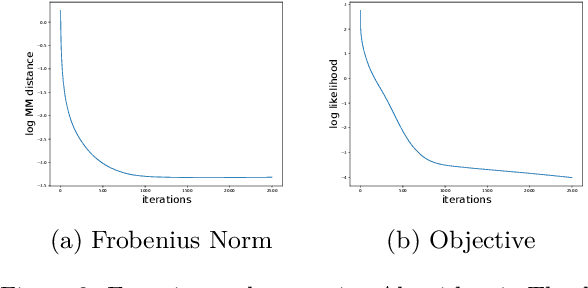
We propose a new topic modeling procedure that takes advantage of the fact that the Latent Dirichlet Allocation (LDA) log likelihood function is asymptotically equivalent to the logarithm of the volume of the topic simplex. This allows topic modeling to be reformulated as finding the probability simplex that minimizes its volume and encloses the documents that are represented as distributions over words. A convex relaxation of the minimum volume topic model optimization is proposed, and it is shown that the relaxed problem has the same global minimum as the original problem under the separability assumption and the sufficiently scattered assumption introduced by Arora et al. (2013) and Huang et al. (2016). A locally convergent alternating direction method of multipliers (ADMM) approach is introduced for solving the relaxed minimum volume problem. Numerical experiments illustrate the benefits of our approach in terms of computation time and topic recovery performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge