Minimum Constraint Removal Problem for Line Segments is NP-hard
Paper and Code
Jul 07, 2021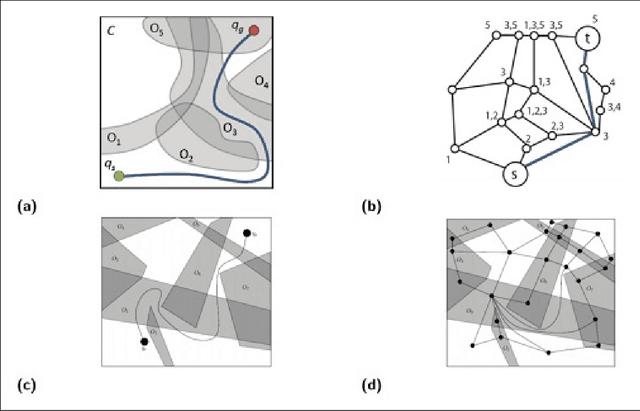
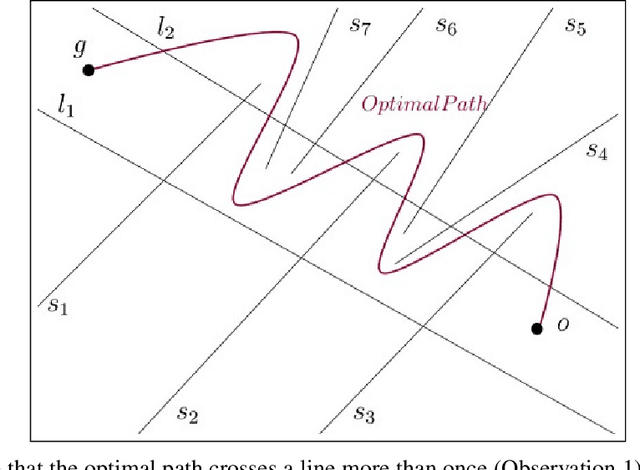
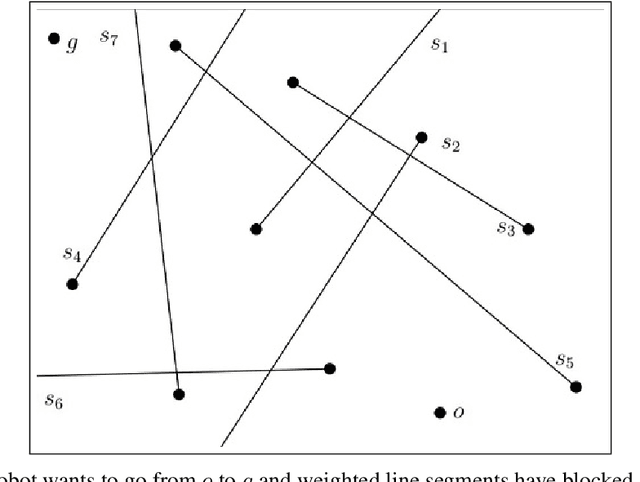
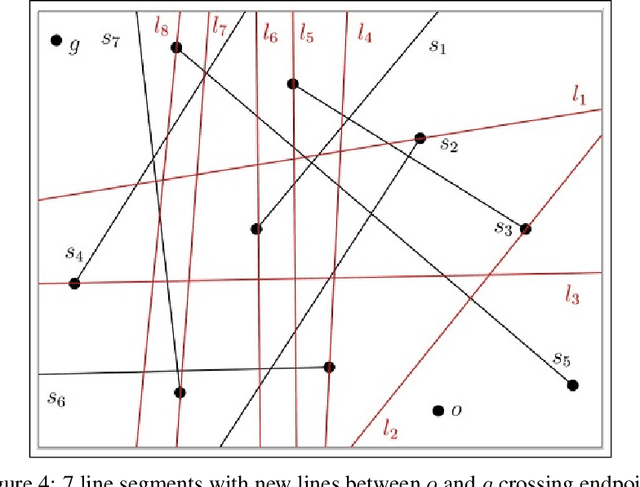
In the minimum constraint removal ($MCR$), there is no feasible path to move from the starting point towards the goal and, the minimum constraints should be removed in order to find a collision-free path. It has been proved that $MCR$ problem is $NP-hard$ when constraints have arbitrary shapes or even they are in shape of convex polygons. However, it has a simple linear solution when constraints are lines and the problem is open for other cases yet. In this paper, using a reduction from Subset Sum problem, in three steps, we show that the problem is NP-hard for both weighted and unweighted line segments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge