Minimizing Close-k Aggregate Loss Improves Classification
Paper and Code
Nov 03, 2018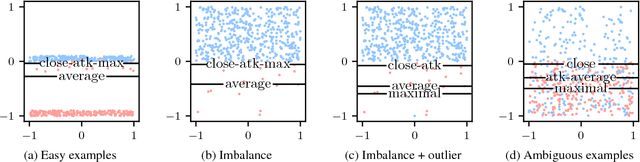
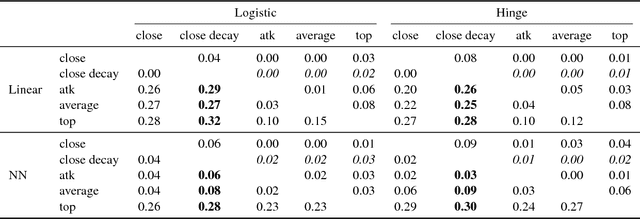
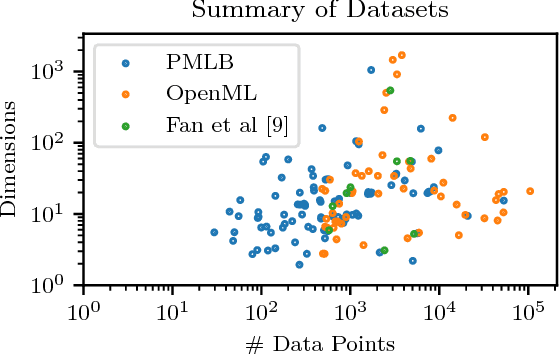

In classification, the de facto method for aggregating individual losses is the average loss. When the actual metric of interest is 0-1 loss, it is common to minimize the average surrogate loss for some well-behaved (e.g. convex) surrogate. Recently, several other aggregate losses such as the maximal loss and average top-$k$ loss were proposed as alternative objectives to address shortcomings of the average loss. However, we identify common classification settings, e.g. the data is imbalanced, has too many easy or ambiguous examples, etc., when average, maximal and average top-$k$ all suffer from suboptimal decision boundaries, even on an infinitely large training set. To address this problem, we propose a new classification objective called the close-$k$ aggregate loss, where we adaptively minimize the loss for points close to the decision boundary. We provide theoretical guarantees for the 0-1 accuracy when we optimize close-$k$ aggregate loss. We also conduct systematic experiments across the PMLB and OpenML benchmark datasets. Close-$k$ achieves significant gains in 0-1 test accuracy, improvements of $\geq 2$% and $p<0.05$, in over 25% of the datasets compared to average, maximal and average top-$k$. In contrast, the previous aggregate losses outperformed close-$k$ in less than 2% of the datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge