Minimal Sample Subspace Learning: Theory and Algorithms
Paper and Code
Jul 13, 2019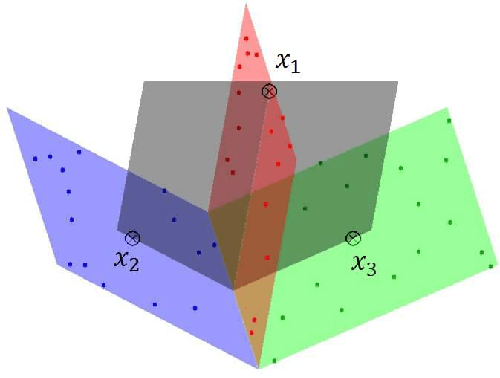
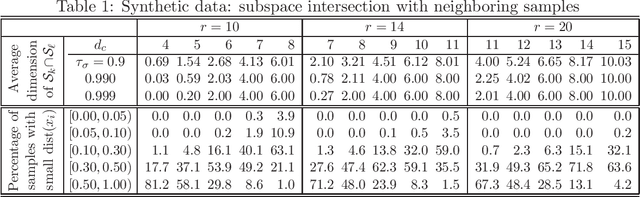
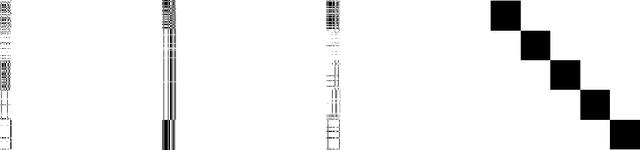

Subspace segmentation or subspace learning is a challenging and complicated task in machine learning. This paper builds a primary frame and solid theoretical bases for the minimal subspace segmentation (MSS) of finite samples. Existence and conditional uniqueness of MSS are discussed with conditions generally satisfied in applications. Utilizing weak prior information of MSS, the minimality inspection of segments is further simplified to the prior detection of partitions. The MSS problem is then modeled as a computable optimization problem via self-expressiveness of samples. A closed form of representation matrices is first given for the self-expressiveness, and the connection of diagonal blocks is then addressed. The MSS model uses a rank restriction on the sum of segment ranks. Theoretically, it can retrieve the minimal sample subspaces that could be heavily intersected. The optimization problem is solved via a basic manifold conjugate gradient algorithm, alternative optimization and hybrid optimization, taking into account of solving both the primal MSS problem and its pseudo-dual problem. The MSS model is further modified for handling noisy data, and solved by an ADMM algorithm. The reported experiments show the strong ability of the MSS method on retrieving minimal sample subspaces that are heavily intersected.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge