Minimal Neural Atlas: Parameterizing Complex Surfaces with Minimal Charts and Distortion
Paper and Code
Jul 29, 2022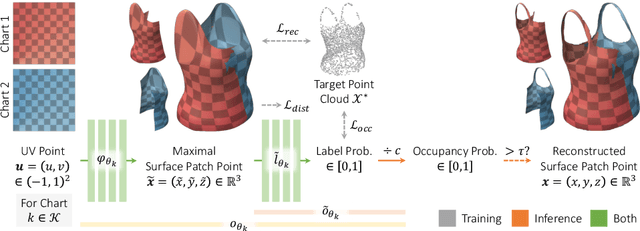
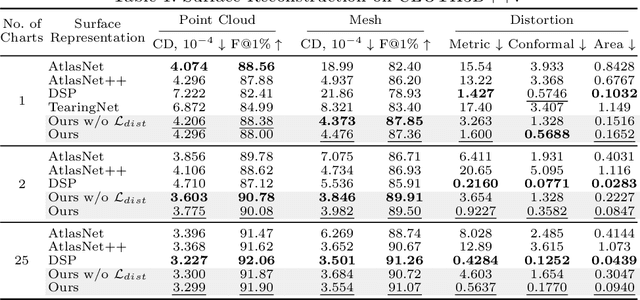
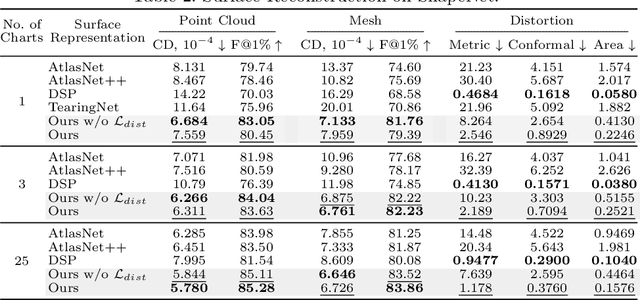
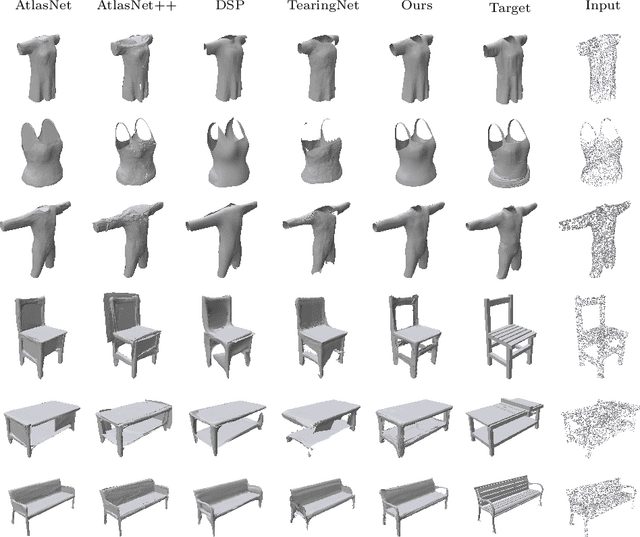
Explicit neural surface representations allow for exact and efficient extraction of the encoded surface at arbitrary precision, as well as analytic derivation of differential geometric properties such as surface normal and curvature. Such desirable properties, which are absent in its implicit counterpart, makes it ideal for various applications in computer vision, graphics and robotics. However, SOTA works are limited in terms of the topology it can effectively describe, distortion it introduces to reconstruct complex surfaces and model efficiency. In this work, we present Minimal Neural Atlas, a novel atlas-based explicit neural surface representation. At its core is a fully learnable parametric domain, given by an implicit probabilistic occupancy field defined on an open square of the parametric space. In contrast, prior works generally predefine the parametric domain. The added flexibility enables charts to admit arbitrary topology and boundary. Thus, our representation can learn a minimal atlas of 3 charts with distortion-minimal parameterization for surfaces of arbitrary topology, including closed and open surfaces with arbitrary connected components. Our experiments support the hypotheses and show that our reconstructions are more accurate in terms of the overall geometry, due to the separation of concerns on topology and geometry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge