Minimal Conditions for Beneficial Neighbourhood Search and Local Descent
Paper and Code
Nov 08, 2024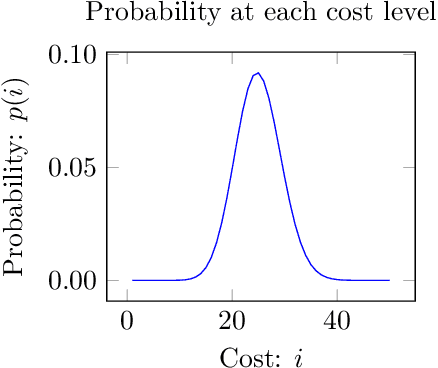
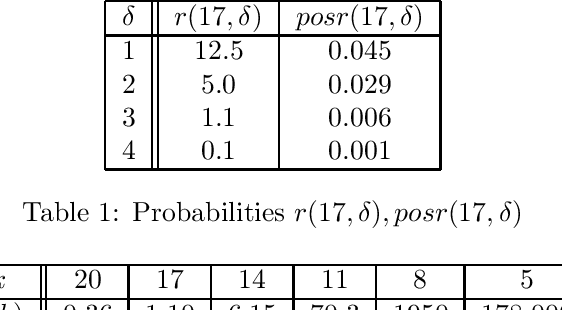
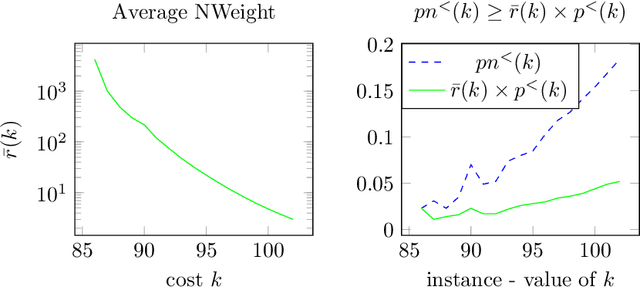
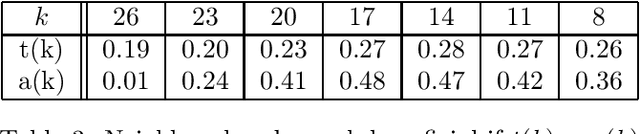
This paper investigates what properties a neighbourhood requires to support beneficial local search. We show that neighbourhood locality, and a reduction in cost probability towards the optimum, support a proof that search among neighbours is more likely to find an improving solution in a single search step than blind search. This is the first paper to introduce such a proof. The concepts underlying these properties are illustrated on a satisfiability problem class, and on travelling salesman problems. Secondly, for a given cost target t, we investigate a combination of blind search and local descent termed local blind descent, and present various conditions under which the expected number of steps to reach a cost better than t using local blind descent, is proven to be smaller than with blind search. Experiments indicate that local blind descent, given target cost t, should switch to local descent at a starting cost that reduces as t approaches the optimum.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge