MGS: Markov Greedy Sums for Accurate Low-Bitwidth Floating-Point Accumulation
Paper and Code
Apr 12, 2025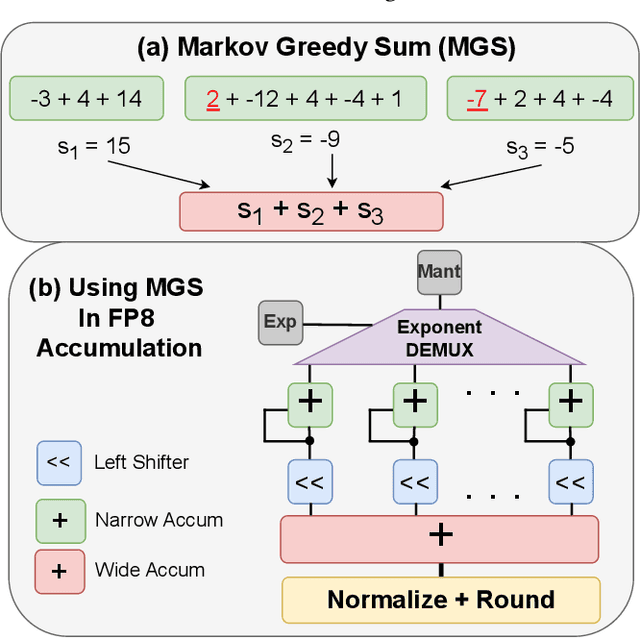

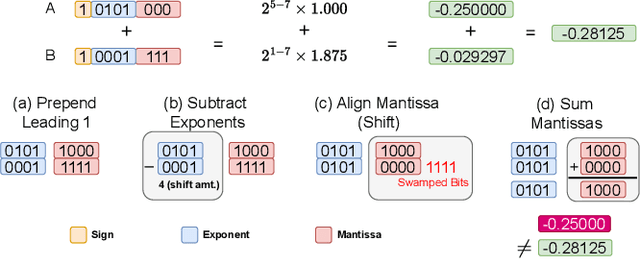
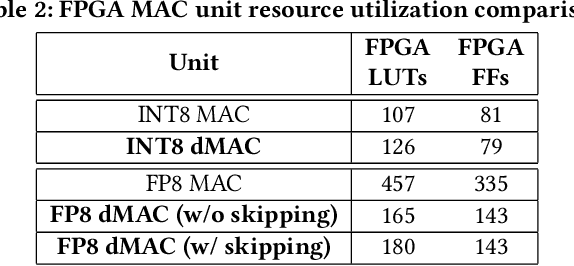
We offer a novel approach, MGS (Markov Greedy Sums), to improve the accuracy of low-bitwidth floating-point dot products in neural network computations. In conventional 32-bit floating-point summation, adding values with different exponents may lead to loss of precision in the mantissa of the smaller term, which is right-shifted to align with the larger term's exponent. Such shifting (a.k.a. 'swamping') is a significant source of numerical errors in accumulation when implementing low-bitwidth dot products (e.g., 8-bit floating point) as the mantissa has a small number of bits. We avoid most swamping errors by arranging the terms in dot product summation based on their exponents and summing the mantissas without overflowing the low-bitwidth accumulator. We design, analyze, and implement the algorithm to minimize 8-bit floating point error at inference time for several neural networks. In contrast to traditional sequential summation, our method has significantly lowered numerical errors, achieving classification accuracy on par with high-precision floating-point baselines for multiple image classification tasks. Our dMAC hardware units can reduce power consumption by up to 34.1\% relative to conventional MAC units.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge