Metric as Transform: Exploring beyond Affine Transform for Interpretable Neural Network
Paper and Code
Oct 21, 2024


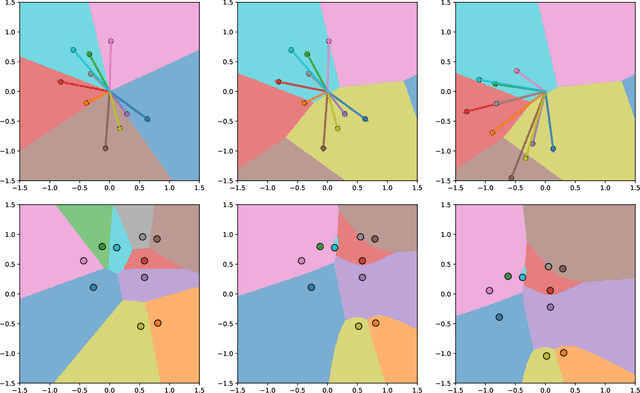
Artificial Neural Networks of varying architectures are generally paired with affine transformation at the core. However, we find dot product neurons with global influence less interpretable as compared to local influence of euclidean distance (as used in Radial Basis Function Network). In this work, we explore the generalization of dot product neurons to $l^p$-norm, metrics, and beyond. We find that metrics as transform performs similarly to affine transform when used in MultiLayer Perceptron or Convolutional Neural Network. Moreover, we explore various properties of Metrics, compare it with Affine, and present multiple cases where metrics seem to provide better interpretability. We develop an interpretable local dictionary based Neural Networks and use it to understand and reject adversarial examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge