Meta-Learning Sparse Compression Networks

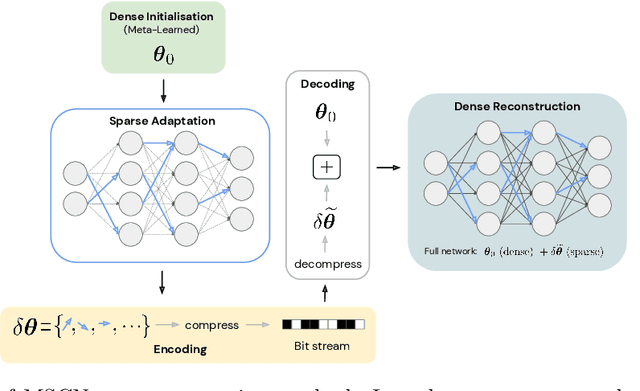
Recent work in Deep Learning has re-imagined the representation of data as functions mapping from a coordinate space to an underlying continuous signal. When such functions are approximated by neural networks this introduces a compelling alternative to the more common multi-dimensional array representation. Recent work on such Implicit Neural Representations (INRs) has shown that - following careful architecture search - INRs can outperform established compression methods such as JPEG (e.g. Dupont et al., 2021). In this paper, we propose crucial steps towards making such ideas scalable: Firstly, we employ stateof-the-art network sparsification techniques to drastically improve compression. Secondly, introduce the first method allowing for sparsification to be employed in the inner-loop of commonly used Meta-Learning algorithms, drastically improving both compression and the computational cost of learning INRs. The generality of this formalism allows us to present results on diverse data modalities such as images, manifolds, signed distance functions, 3D shapes and scenes, several of which establish new state-of-the-art results.