Meta-Learning Guarantees for Online Receding Horizon Control
Paper and Code
Nov 11, 2020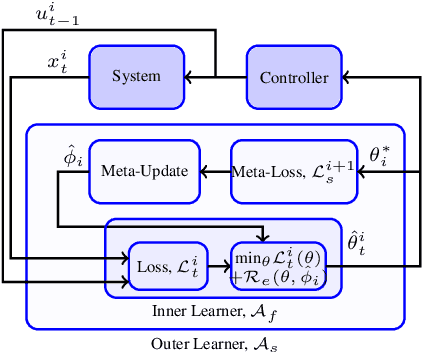
In this paper we provide provable regret guarantees for an online meta-learning receding horizon control algorithm in an iterative control setting, where in each iteration the system to be controlled is a linear deterministic system that is different and unknown, the cost for the controller in an iteration is a general additive cost function and the control input is required to be constrained, which if violated incurs an additional cost. We prove (i) that the algorithm achieves a regret for the controller cost and constraint violation that are $O(T^{3/4})$ for an episode of duration $T$ with respect to the best policy that satisfies the control input control constraints and (ii) that the average of the regret for the controller cost and constraint violation with respect to the same policy vary as $O((1+1/\sqrt{N})T^{3/4})$ with the number of iterations $N$, showing that the worst regret for the learning within an iteration continuously improves with experience of more iterations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge