Measuring spatial uniformity with the hypersphere chord length distribution
Paper and Code
Apr 12, 2020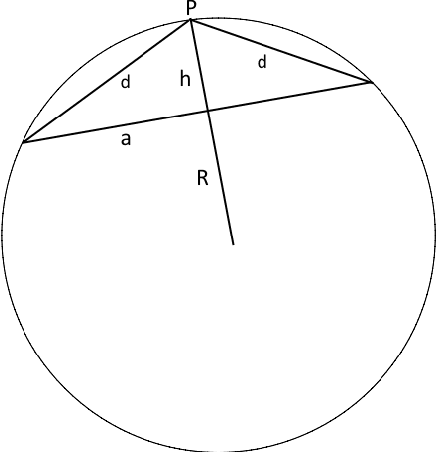
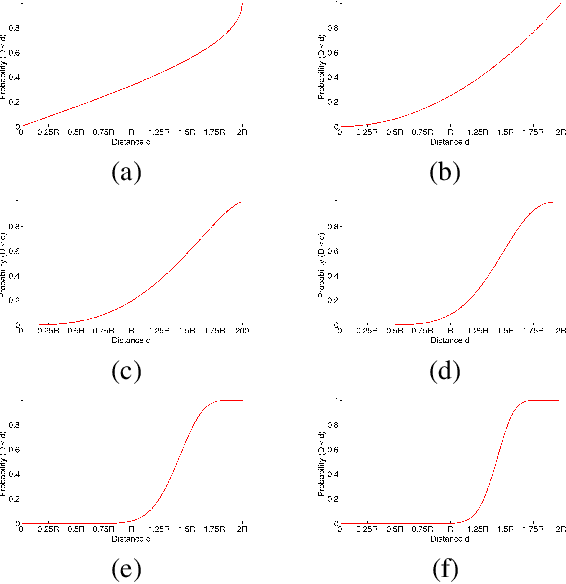
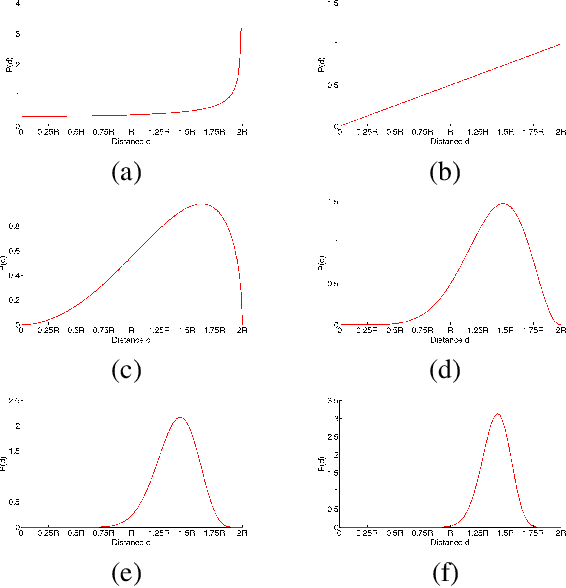
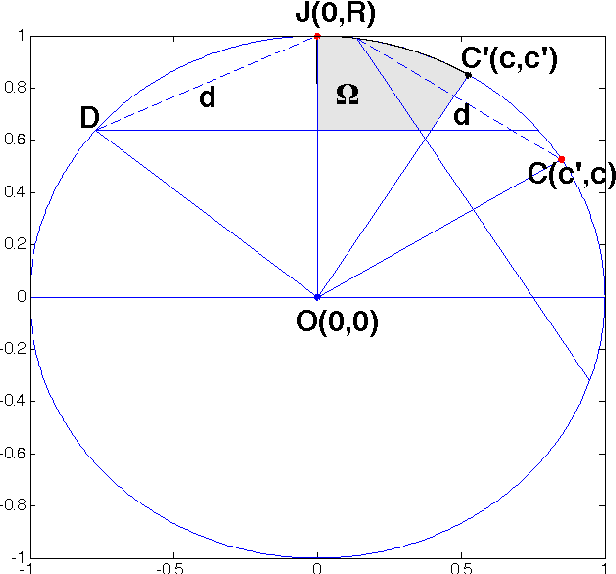
Data uniformity is a concept associated with several semantic data characteristics such as lack of features, correlation and sample bias. This article introduces a novel measure to assess data uniformity and detect uniform pointsets on high-dimensional Euclidean spaces. Spatial uniformity measure builds upon the isomorphism between hyperspherical chords and L2-normalised data Euclidean distances, which is implied by the fact that, in Euclidean spaces, L2-normalised data can be geometrically defined as points on a hypersphere. The imposed connection between the distance distribution of uniformly selected points and the hyperspherical chord length distribution is employed to quantify uniformity. More specifically,, the closed-form expression of hypersphere chord length distribution is revisited extended, before examining a few qualitative and quantitative characteristics of this distribution that can be rather straightforwardly linked to data uniformity. The experimental section includes validation in four distinct setups, thus substantiating the potential of the new uniformity measure on practical data-science applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge