Maximum Margin Principal Components
Paper and Code
May 17, 2017
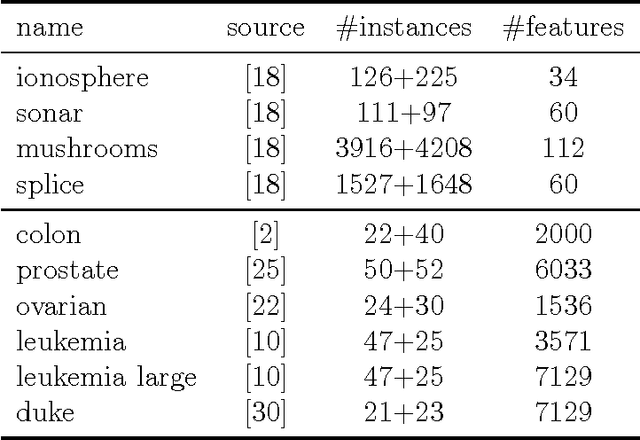

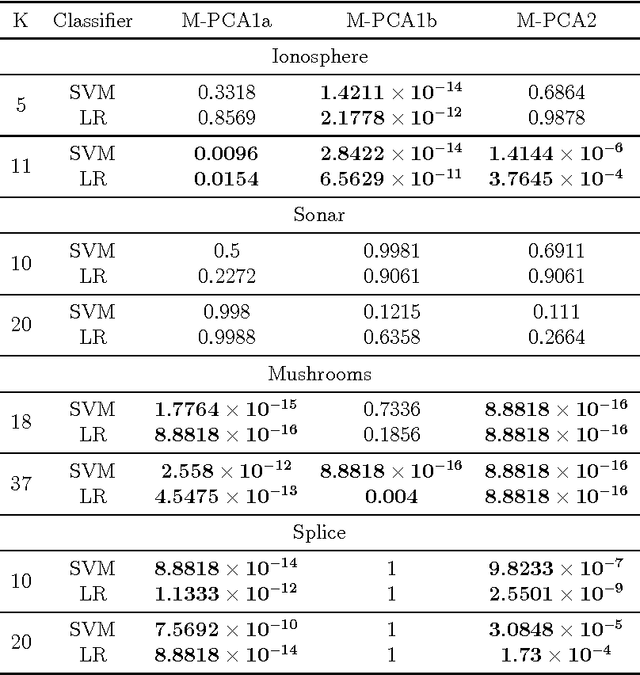
Principal Component Analysis (PCA) is a very successful dimensionality reduction technique, widely used in predictive modeling. A key factor in its widespread use in this domain is the fact that the projection of a dataset onto its first $K$ principal components minimizes the sum of squared errors between the original data and the projected data over all possible rank $K$ projections. Thus, PCA provides optimal low-rank representations of data for least-squares linear regression under standard modeling assumptions. On the other hand, when the loss function for a prediction problem is not the least-squares error, PCA is typically a heuristic choice of dimensionality reduction -- in particular for classification problems under the zero-one loss. In this paper we target classification problems by proposing a straightforward alternative to PCA that aims to minimize the difference in margin distribution between the original and the projected data. Extensive experiments show that our simple approach typically outperforms PCA on any particular dataset, in terms of classification error, though this difference is not always statistically significant, and despite being a filter method is frequently competitive with Partial Least Squares (PLS) and Lasso on a wide range of datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge