Markov Random Fields for Collaborative Filtering
Paper and Code
Oct 21, 2019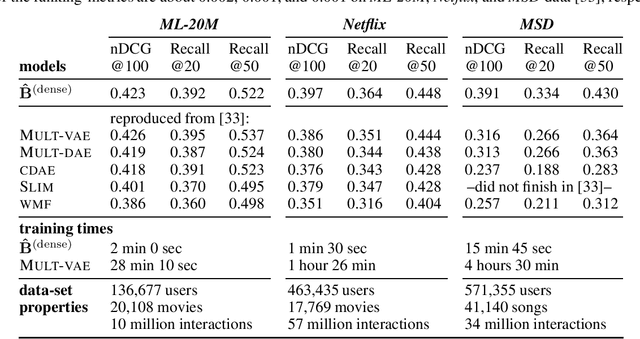
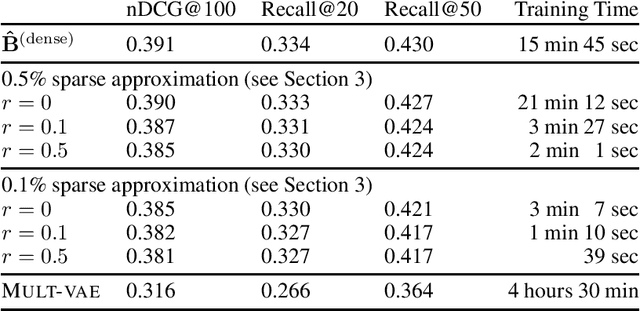
In this paper, we model the dependencies among the items that are recommended to a user in a collaborative-filtering problem via a Gaussian Markov Random Field (MRF). We build upon Besag's auto-normal parameterization and pseudo-likelihood, which not only enables computationally efficient learning, but also connects the areas of MRFs and sparse inverse covariance estimation with autoencoders and neighborhood models, two successful approaches in collaborative filtering. We propose a novel approximation for learning sparse MRFs, where the trade-off between recommendation-accuracy and training-time can be controlled. At only a small fraction of the training-time compared to various baselines, including deep nonlinear models, the proposed approach achieved competitive ranking-accuracy on all three well-known data-sets used in our experiments, and notably a 20% gain in accuracy on the data-set with the largest number of items.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge