Manipulating Reinforcement Learning: Poisoning Attacks on Cost Signals
Paper and Code
Feb 07, 2020

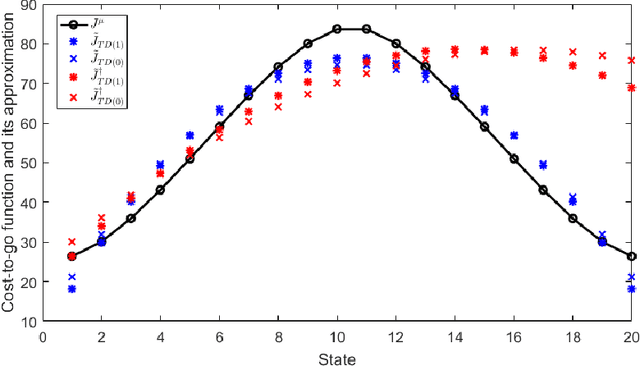
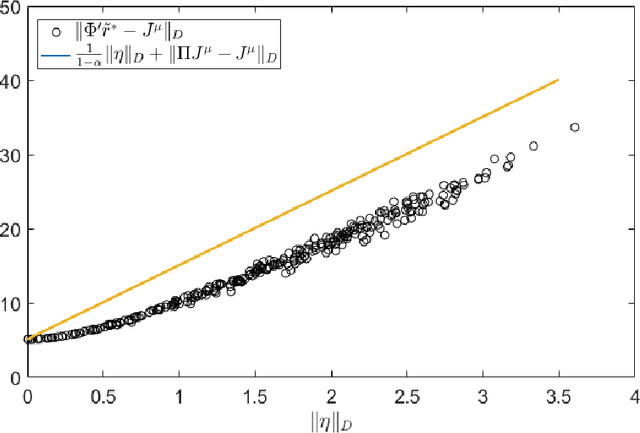
This chapter studies emerging cyber-attacks on reinforcement learning (RL) and introduces a quantitative approach to analyze the vulnerabilities of RL. Focusing on adversarial manipulation on the cost signals, we analyze the performance degradation of TD($\lambda$) and $Q$-learning algorithms under the manipulation. For TD($\lambda$), the approximation learned from the manipulated costs has an approximation error bound proportional to the magnitude of the attack. The effect of the adversarial attacks on the bound does not depend on the choice of $\lambda$. In $Q$-learning, we show that $Q$-learning algorithms converge under stealthy attacks and bounded falsifications on cost signals. We characterize the relation between the falsified cost and the $Q$-factors as well as the policy learned by the learning agent which provides fundamental limits for feasible offensive and defensive moves. We propose a robust region in terms of the cost within which the adversary can never achieve the targeted policy. We provide conditions on the falsified cost which can mislead the agent to learn an adversary's favored policy. A case study of TD($\lambda$) learning is provided to corroborate the results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge