MANI-Rank: Multiple Attribute and Intersectional Group Fairness for Consensus Ranking
Paper and Code
Jul 20, 2022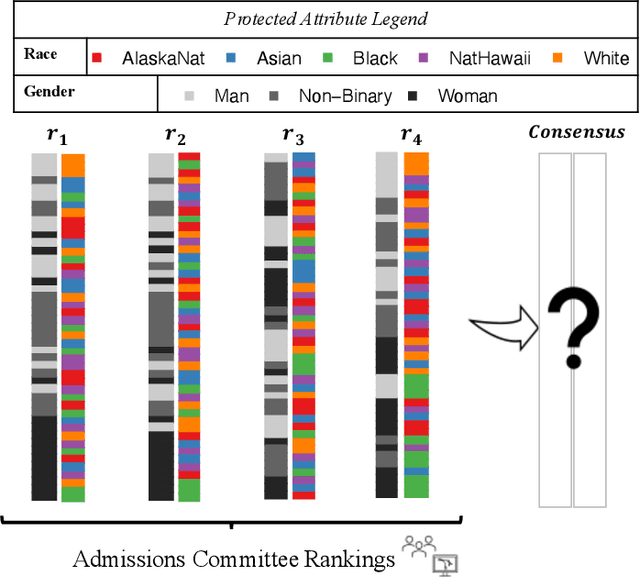

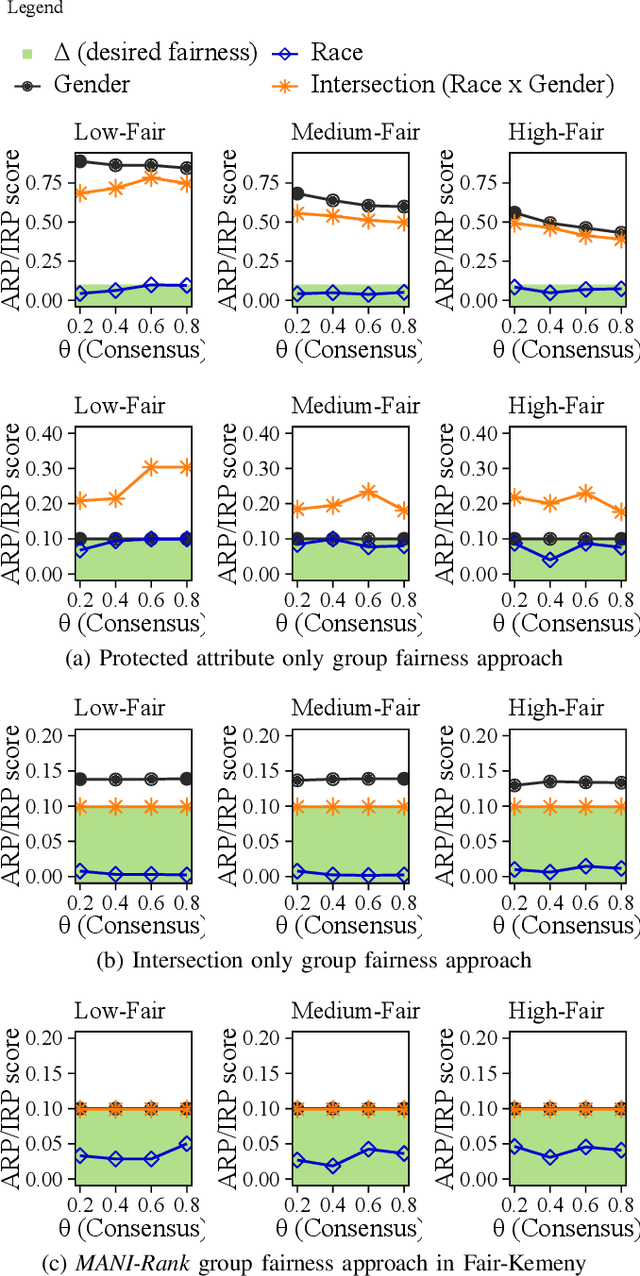
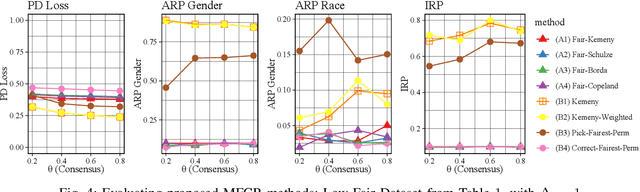
Combining the preferences of many rankers into one single consensus ranking is critical for consequential applications from hiring and admissions to lending. While group fairness has been extensively studied for classification, group fairness in rankings and in particular rank aggregation remains in its infancy. Recent work introduced the concept of fair rank aggregation for combining rankings but restricted to the case when candidates have a single binary protected attribute, i.e., they fall into two groups only. Yet it remains an open problem how to create a consensus ranking that represents the preferences of all rankers while ensuring fair treatment for candidates with multiple protected attributes such as gender, race, and nationality. In this work, we are the first to define and solve this open Multi-attribute Fair Consensus Ranking (MFCR) problem. As a foundation, we design novel group fairness criteria for rankings, called MANI-RANK, ensuring fair treatment of groups defined by individual protected attributes and their intersection. Leveraging the MANI-RANK criteria, we develop a series of algorithms that for the first time tackle the MFCR problem. Our experimental study with a rich variety of consensus scenarios demonstrates our MFCR methodology is the only approach to achieve both intersectional and protected attribute fairness while also representing the preferences expressed through many base rankings. Our real-world case study on merit scholarships illustrates the effectiveness of our MFCR methods to mitigate bias across multiple protected attributes and their intersections. This is an extended version of "MANI-Rank: Multiple Attribute and Intersectional Group Fairness for Consensus Ranking", to appear in ICDE 2022.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge