Making a Mess and Getting Away with it: Traveling Salesperson Problem with Circle Placement for Dubins Vehicles

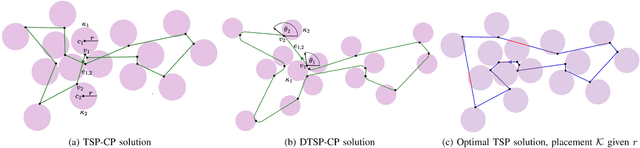
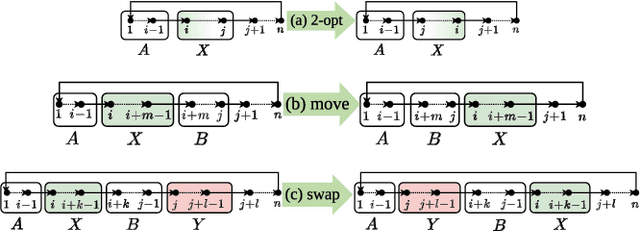
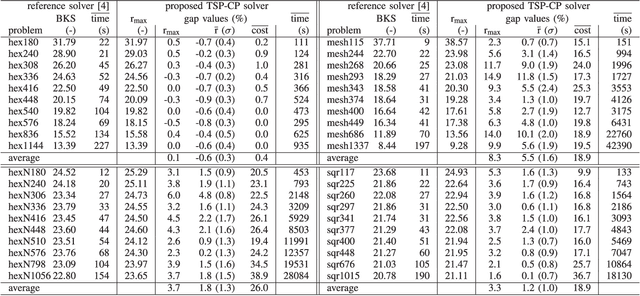
This paper explores a variation of the Traveling Salesperson Problem, where the agent places a circular obstacle next to each node once it visits it. Referred to as the Traveling Salesperson Problem with Circle Placement (TSP-CP), the aim is to maximize the obstacle radius for which a valid closed tour exists and then minimize the tour cost. The TSP-CP finds relevance in various real-world applications, such as harvesting, quarrying, and open-pit mining. We propose several novel solvers to address the TSP-CP, its variant tailored for Dubins vehicles, and a crucial subproblem known as the Traveling Salesperson Problem on self-deleting graphs (TSP-SD). Our extensive experimental results show that the proposed solvers outperform the current state-of-the-art on related problems in solution quality.