Machine learning Calabi-Yau metrics
Paper and Code
Oct 18, 2019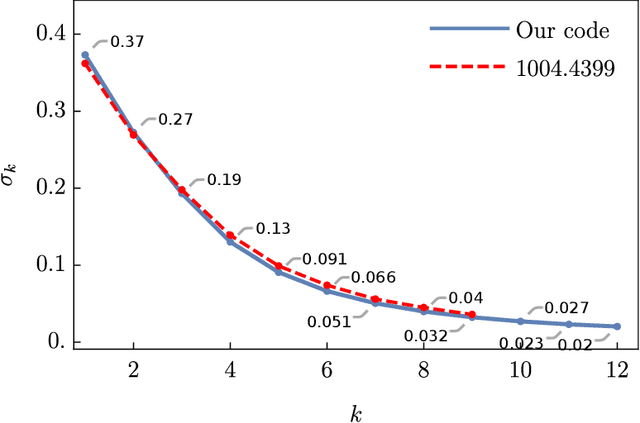
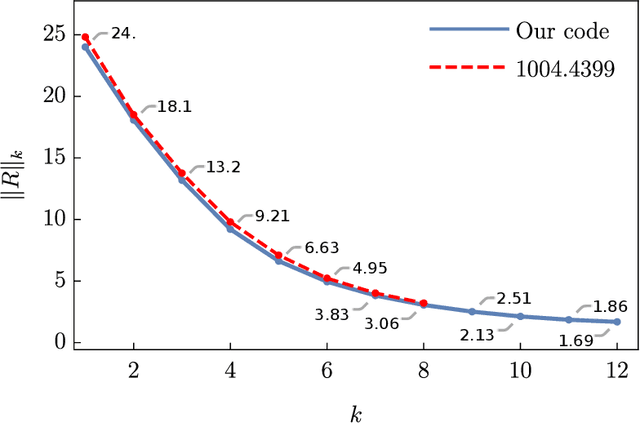
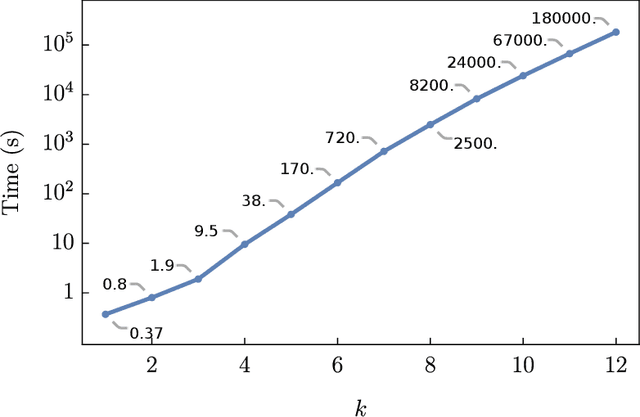
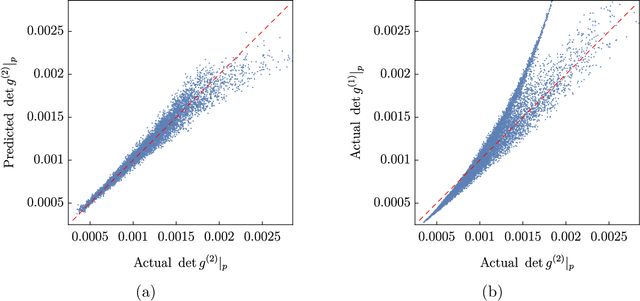
We apply machine learning to the problem of finding numerical Calabi-Yau metrics. Building on Donaldson's algorithm for calculating balanced metrics on K\"ahler manifolds, we combine conventional curve fitting and machine-learning techniques to numerically approximate Ricci-flat metrics. We show that machine learning is able to predict the Calabi-Yau metric and quantities associated with it, such as its determinant, having seen only a small sample of training data. Using this in conjunction with a straightforward curve fitting routine, we demonstrate that it is possible to find highly accurate numerical metrics much more quickly than by using Donaldson's algorithm alone, with our new machine-learning algorithm decreasing the time required by between one and two orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge