LSTM Networks Can Perform Dynamic Counting
Paper and Code
Jun 09, 2019
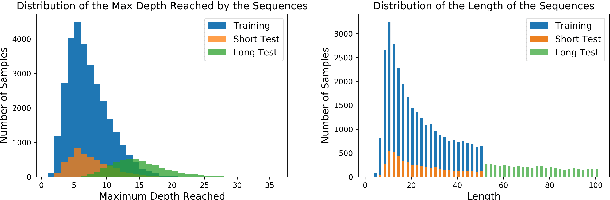

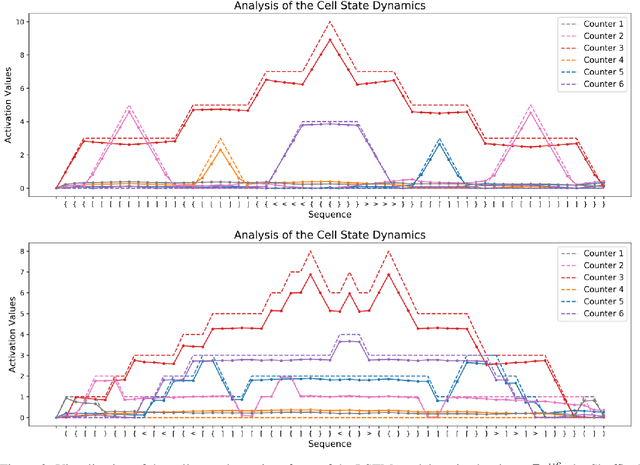
In this paper, we systematically assess the ability of standard recurrent networks to perform dynamic counting and to encode hierarchical representations. All the neural models in our experiments are designed to be small-sized networks both to prevent them from memorizing the training sets and to visualize and interpret their behaviour at test time. Our results demonstrate that the Long Short-Term Memory (LSTM) networks can learn to recognize the well-balanced parenthesis language (Dyck-$1$) and the shuffles of multiple Dyck-$1$ languages, each defined over different parenthesis-pairs, by emulating simple real-time $k$-counter machines. To the best of our knowledge, this work is the first study to introduce the shuffle languages to analyze the computational power of neural networks. We also show that a single-layer LSTM with only one hidden unit is practically sufficient for recognizing the Dyck-$1$ language. However, none of our recurrent networks was able to yield a good performance on the Dyck-$2$ language learning task, which requires a model to have a stack-like mechanism for recognition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge