Low-Rank Tensor Completion With Generalized CP Decomposition and Nonnegative Integer Tensor Completion
Paper and Code
Feb 12, 2023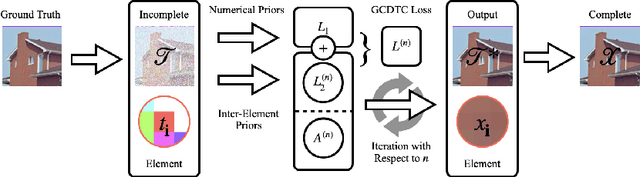
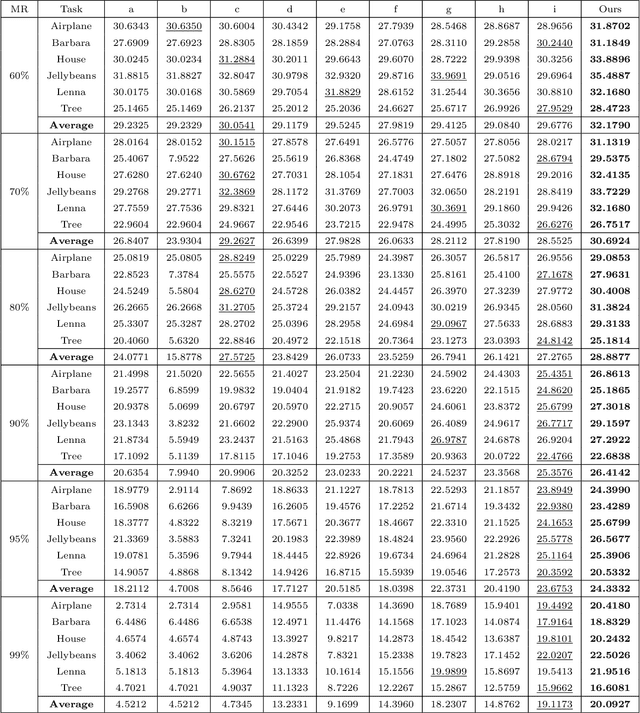
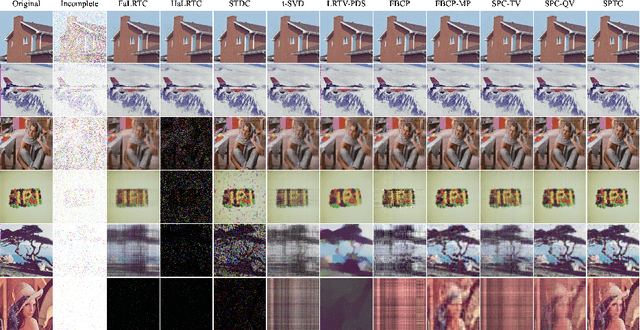

The problem of tensor completion is important to many areas such as computer vision, data analysis, signal processing, etc. Previously, a category of methods known as low-rank tensor completion has been proposed and developed, involving the enforcement of low-rank structures on completed tensors. While such methods have been constantly improved, none have previously considered exploiting the numerical properties of tensor elements. This work attempts to construct a new methodological framework called GCDTC (Generalized CP Decomposition Tensor Completion) based on these properties. In this newly introduced framework, the CP Decomposition is reformulated as a Maximum Likelihood Estimate (MLE) problem, and generalized via the introduction of differing loss functions. The generalized decomposition is subsequently applied to low-rank tensor completion. Such loss functions can also be easily adjusted to consider additional factors in completion, such as smoothness, standardization, etc. An example of nonnegative integer tensor decomposition via the Poisson CP Decomposition is given to demonstrate the new methodology's potentials. Through experimentation with real-life data, it is confirmed that this method could produce results superior to current state-of-the-art methodologies. It is expected that the proposed notion would inspire a new set of tensor completion methods based on the generalization of decompositions, thus contributing to related fields.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge