Low-rank Meets Sparseness: An Integrated Spatial-Spectral Total Variation Approach to Hyperspectral Denoising

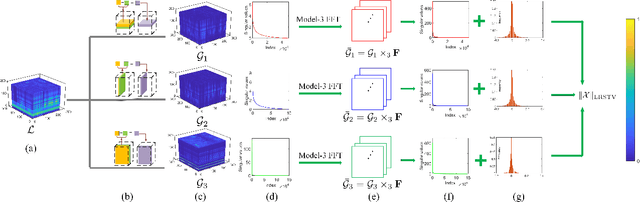
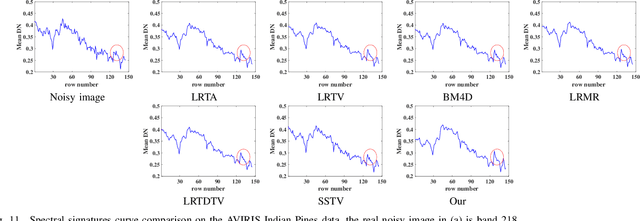
Spatial-Spectral Total Variation (SSTV) can quantify local smoothness of image structures, so it is widely used in hyperspectral image (HSI) processing tasks. Essentially, SSTV assumes a sparse structure of gradient maps calculated along the spatial and spectral directions. In fact, these gradient tensors are not only sparse, but also (approximately) low-rank under FFT, which we have verified by numerical tests and theoretical analysis. Based on this fact, we propose a novel TV regularization to simultaneously characterize the sparsity and low-rank priors of the gradient map (LRSTV). The new regularization not only imposes sparsity on the gradient map itself, but also penalize the rank on the gradient map after Fourier transform along the spectral dimension. It naturally encodes the sparsity and lowrank priors of the gradient map, and thus is expected to reflect the inherent structure of the original image more faithfully. Further, we use LRSTV to replace conventional SSTV and embed it in the HSI processing model to improve its performance. Experimental results on multiple public data-sets with heavy mixed noise show that the proposed model can get 1.5dB improvement of PSNR.