Low-Rank Approximation of Structural Redundancy for Self-Supervised Learning

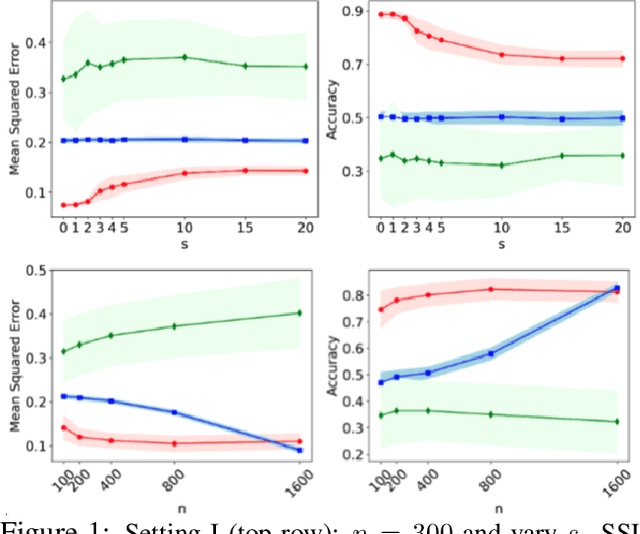
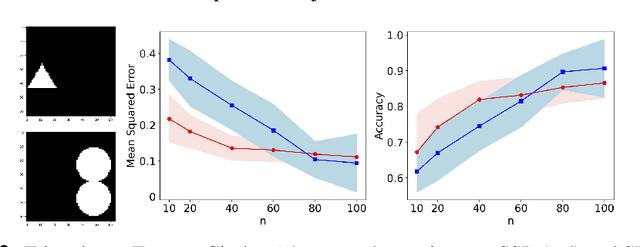
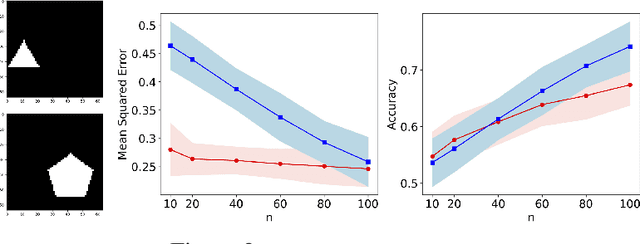
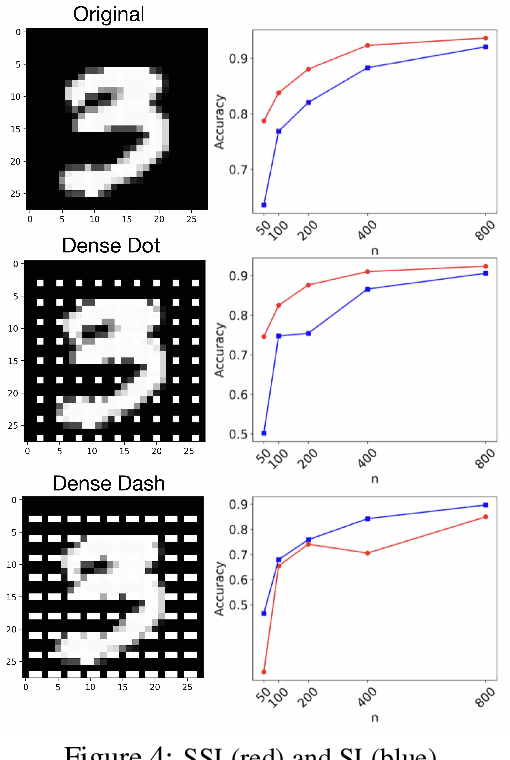
We study the data-generating mechanism for reconstructive SSL to shed light on its effectiveness. With an infinite amount of labeled samples, we provide a sufficient and necessary condition for perfect linear approximation. The condition reveals a full-rank component that preserves the label classes of Y, along with a redundant component. Motivated by the condition, we propose to approximate the redundant component by a low-rank factorization and measure the approximation quality by introducing a new quantity $\epsilon_s$, parameterized by the rank of factorization s. We incorporate $\epsilon_s$ into the excess risk analysis under both linear regression and ridge regression settings, where the latter regularization approach is to handle scenarios when the dimension of the learned features is much larger than the number of labeled samples n for downstream tasks. We design three stylized experiments to compare SSL with supervised learning under different settings to support our theoretical findings.