Low-Complexity Data-Parallel Earth Mover's Distance Approximations
Paper and Code
Dec 05, 2018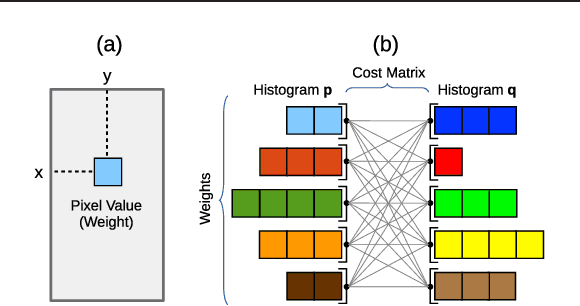
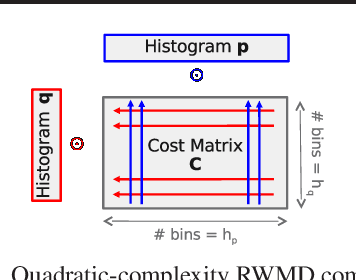
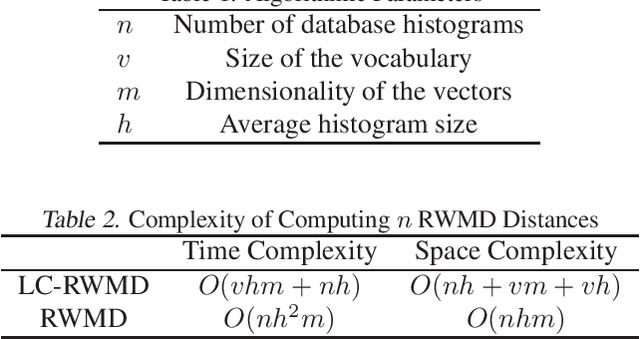
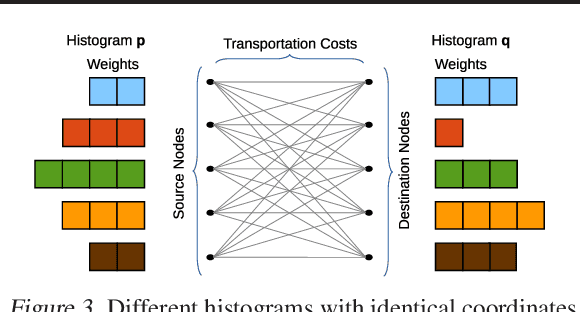
The Earth Mover's Distance (EMD) is a state-of-the art metric for comparing probability distributions. The high distinguishability offered by the EMD comes at a high cost in computational complexity. Therefore, linear-complexity approximation algorithms have been proposed to improve its scalability. However, these algorithms are either limited to vector spaces with only a few dimensions or require the probability distributions to populate the vector space sparsely. We propose novel approximation algorithms that overcome both of these limitations, yet still achieve linear time complexity. All our algorithms are data parallel, and therefore, we can take advantage of massively parallel computing engines, such as Graphics Processing Units (GPUs). The experiments on MNIST images show that the new algorithms can perform a billion distance computations in less than a minute using a single GPU. On the popular text-based 20 Newsgroups dataset, the new algorithms are four orders of magnitude faster than the state-of-the-art FastEMD library and match its search accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge