LocoProp: Enhancing BackProp via Local Loss Optimization

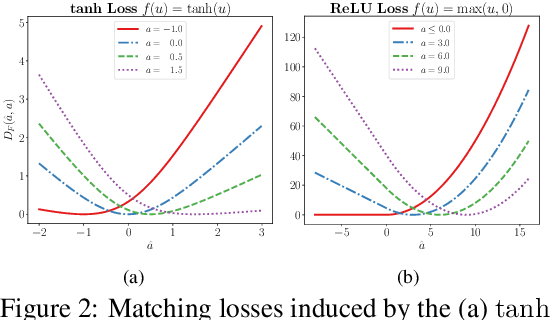
We study a local loss construction approach for optimizing neural networks. We start by motivating the problem as minimizing a squared loss between the pre-activations of each layer and a local target, plus a regularizer term on the weights. The targets are chosen so that the first gradient descent step on the local objectives recovers vanilla BackProp, while the exact solution to each problem results in a preconditioned gradient update. We improve the local loss construction by forming a Bregman divergence in each layer tailored to the transfer function which keeps the local problem convex w.r.t. the weights. The generalized local problem is again solved iteratively by taking small gradient descent steps on the weights, for which the first step recovers BackProp. We run several ablations and show that our construction consistently improves convergence, reducing the gap between first-order and second-order methods.