Local Neighbor Propagation Embedding

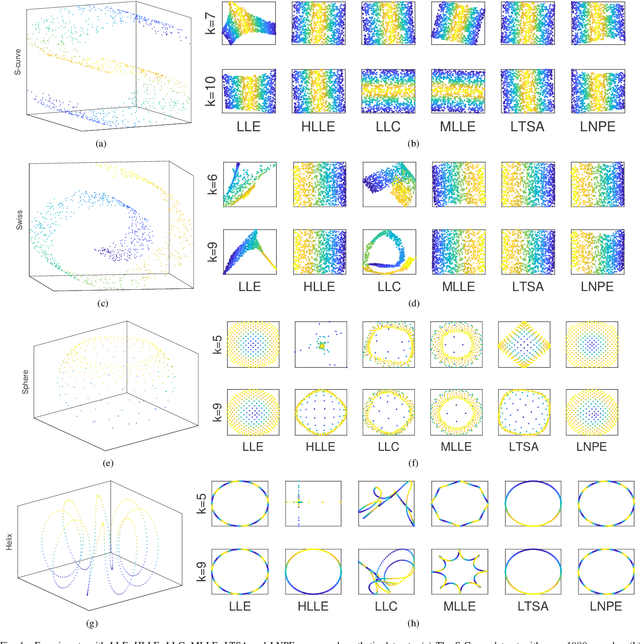
Manifold Learning occupies a vital role in the field of nonlinear dimensionality reduction and its ideas also serve for other relevant methods. Graph-based methods such as Graph Convolutional Networks (GCN) show ideas in common with manifold learning, although they belong to different fields. Inspired by GCN, we introduce neighbor propagation into LLE and propose Local Neighbor Propagation Embedding (LNPE). With linear computational complexity increase compared with LLE, LNPE enhances the local connections and interactions between neighborhoods by extending $1$-hop neighbors into $n$-hop neighbors. The experimental results show that LNPE could obtain more faithful and robust embeddings with better topological and geometrical properties.