Local Fourier Slice Photography

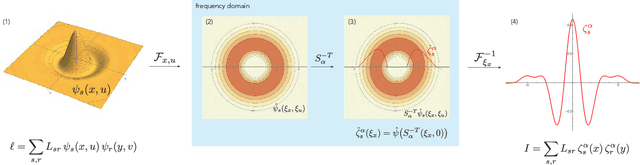
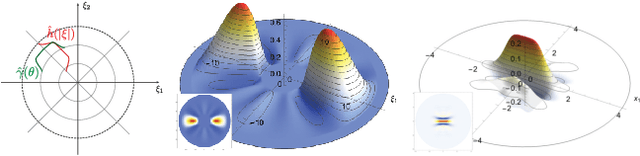
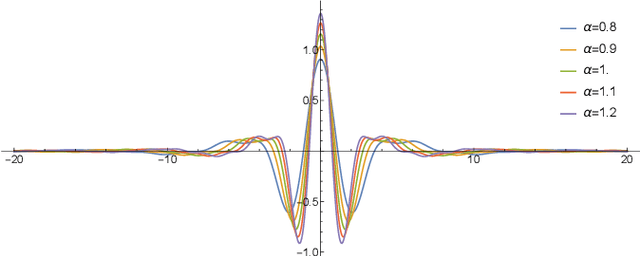
Light field cameras provide intriguing possibilities, such as post-capture refocus or the ability to look behind an object. This comes, however, at the price of significant storage requirements. Compression techniques can be used to reduce these but refocusing and reconstruction require so far again a dense representation. To avoid this, we introduce a sheared local Fourier slice equation that allows for refocusing directly from a compressed light field, either to obtain an image or a compressed representation of it. The result is made possible by wavelets that respect the "slicing's" intrinsic structure and enable us to derive exact reconstruction filters for the refocused image in closed form. Image reconstruction then amounts to applying these filters to the light field's wavelet coefficients, and hence no decompression is necessary. We demonstrate that this substantially reduces storage requirements and also computation times. We furthermore analyze the computational complexity of our algorithm and show that it scales linearly with the size of the reconstructed region and the non-negligible wavelet coefficients, i.e. with the visual complexity.