Local Competition and Uncertainty for Adversarial Robustness in Deep Learning
Paper and Code
Jun 18, 2020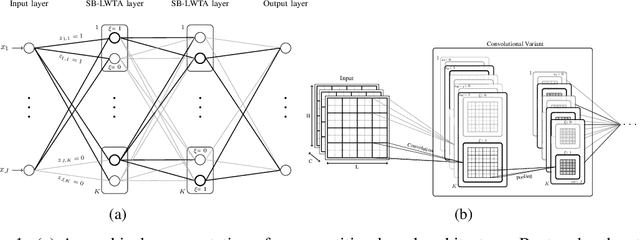
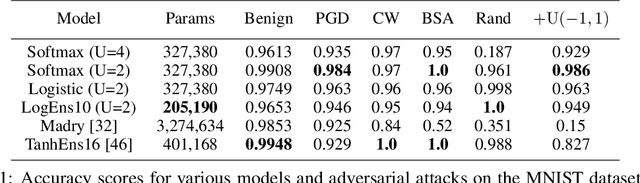
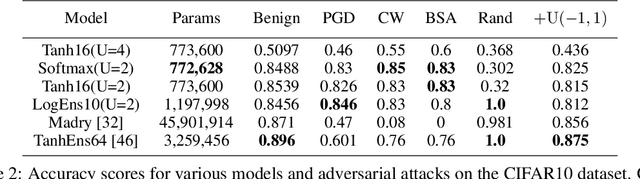
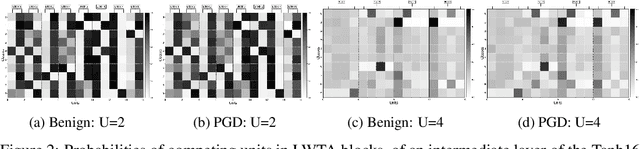
This work attempts to address adversarial robustness of deep networks by means of novel learning arguments. Specifically, inspired from results in neuroscience, we propose a local competition principle as a means of adversarially-robust deep learning. We argue that novel local winner-takes-all (LWTA) nonlinearities, combined with posterior sampling schemes, can greatly improve the adversarial robustness of traditional deep networks against difficult adversarial attack schemes. We combine these LWTA arguments with tools from the field of Bayesian non-parametrics, specifically the stick-breaking construction of the Indian Buffet Process, to flexibly account for the inherent uncertainty in data-driven modeling. As we experimentally show, the new proposed model achieves high robustness to adversarial perturbations on MNIST and CIFAR10 datasets. Our model achieves state-of-the-art results in powerful white-box attacks, while at the same time retaining its benign accuracy to a high degree. Equally importantly, our approach achieves this result while requiring far less trainable model parameters than the existing state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge