Local Change Point Detection and Signal Cleaning using EEMD with applications to Acoustic Shockwaves and Cardiac Signals
Paper and Code
Mar 01, 2021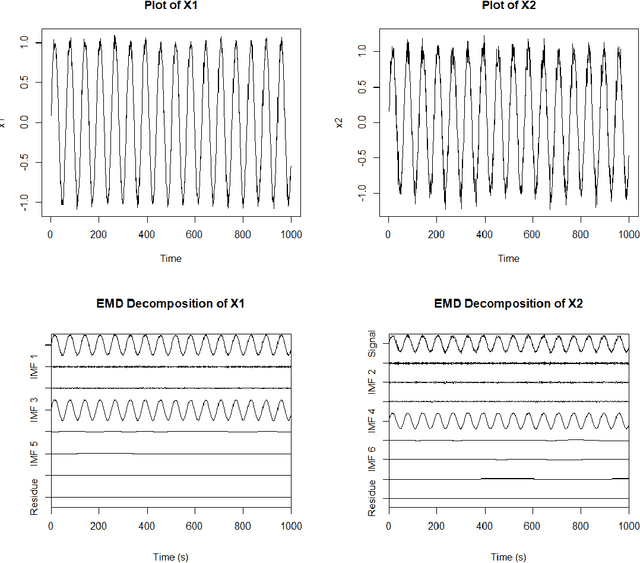



With the ability to create time varying basis functions, the Ensemble Empirical Mode Decomposition (EEMD) has quickly become the preferred way to decompose nonlinear and nonstationary signals. However, we find current EEMD signal cleaning techniques lacking, unable to deal with the nonlinearities that are common for the complex signals that the EEMD is used for. By combining change point detection and a new sparse basis function optimization problem, we are able to show that it is possible to create unique filters for each change point which emphasize the basis functions that are observing a change. This not only allows one to understand which frequency bands are observing a change, but cleaning the signal to emphasize changes can lead to improved signal classification accuracy. We show that this technique has implications for a variety of applications including acoustics and medicine. The technique is implemented in R via the \textbf{LCDSC} package.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge