Linguists Who Use Probabilistic Models Love Them: Quantification in Functional Distributional Semantics
Paper and Code
Jun 04, 2020
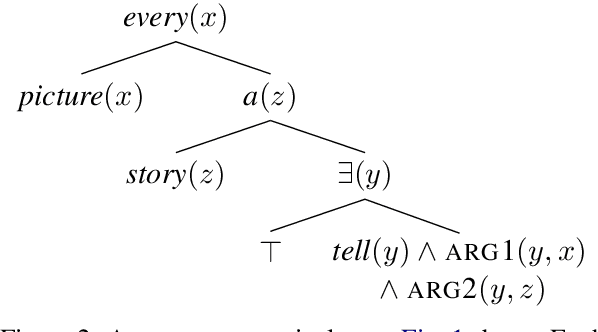


Functional Distributional Semantics provides a computationally tractable framework for learning truth-conditional semantics from a corpus. Previous work in this framework has provided a probabilistic version of first-order logic, recasting quantification as Bayesian inference. In this paper, I show how the previous formulation gives trivial truth values when a precise quantifier is used with vague predicates. I propose an improved account, avoiding this problem by treating a vague predicate as a distribution over precise predicates. I connect this account to recent work in the Rational Speech Acts framework on modelling generic quantification, and I extend this to modelling donkey sentences. Finally, I explain how the generic quantifier can be both pragmatically complex and yet computationally simpler than precise quantifiers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge