Linguistic Fuzzy Information Evolution with Random Leader Election Mechanism for Decision-Making Systems

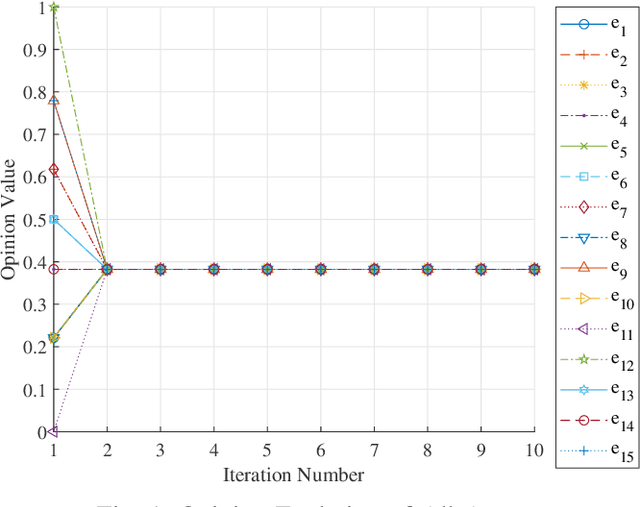
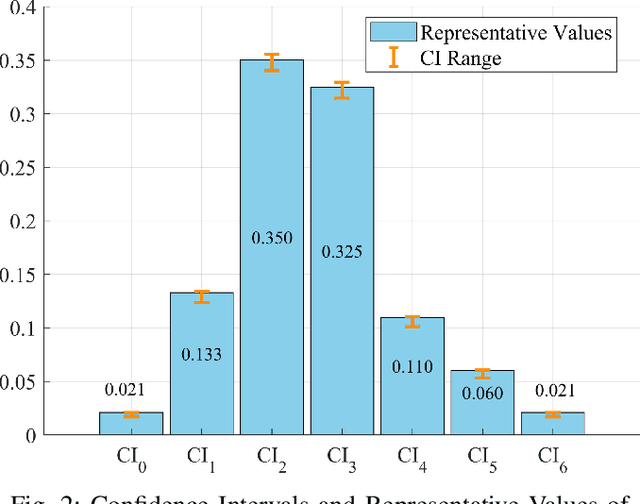
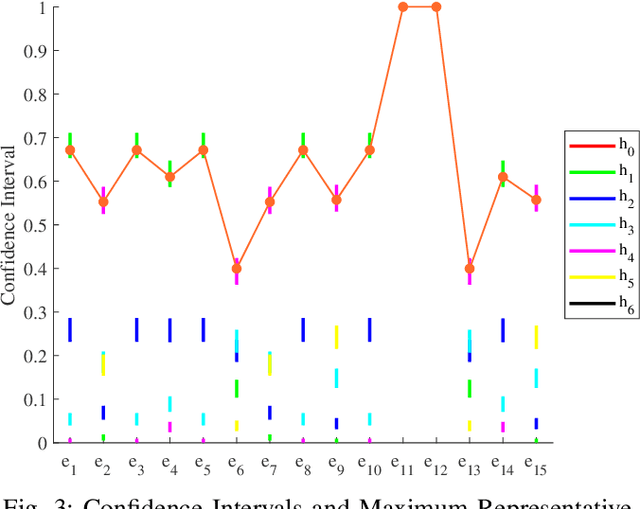
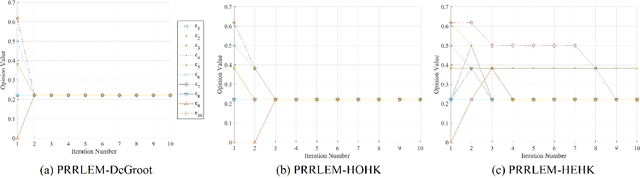
Linguistic fuzzy information evolution is crucial in understanding information exchange among agents. However, different agent weights may lead to different convergence results in the classic DeGroot model. Similarly, in the Hegselmann-Krause bounded confidence model (HK model), changing the confidence threshold values of agents can lead to differences in the final results. To address these limitations, this paper proposes three new models of linguistic fuzzy information dynamics: the per-round random leader election mechanism-based DeGroot model (PRRLEM-DeGroot), the PRRLEM-based homogeneous HK model (PRRLEM-HOHK), and the PRRLEM-based heterogeneous HK model (PRRLEM-HEHK). In these models, after each round of fuzzy information updates, an agent is randomly selected to act as a temporary leader with more significant influence, with the leadership structure being reset after each update. This strategy increases the information sharing and enhances decision-making by integrating multiple agents' evaluation information, which is also in line with real life (\emph{Leader is not unchanged}). The Monte Carlo method is then employed to simulate the behavior of complex systems through repeated random tests, obtaining confidence intervals for different fuzzy information. Subsequently, an improved golden rule representative value (GRRV) in fuzzy theory is proposed to rank these confidence intervals. Simulation examples and a real-world scenario about space situational awareness validate the effectiveness of the proposed models. Comparative analysis with the other models demonstrate our ability to address the echo chamber and improve the robustness.