Linear Model with Local Differential Privacy
Paper and Code
Feb 05, 2022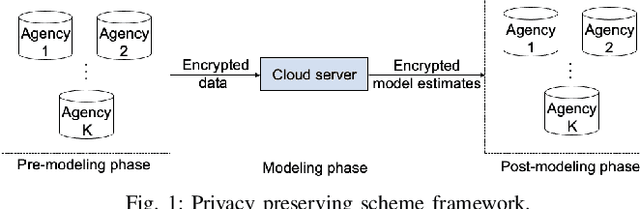
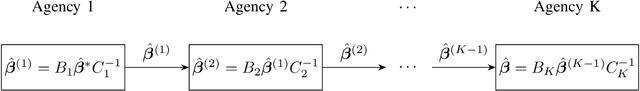
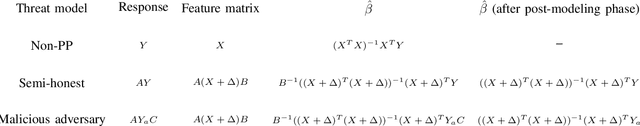
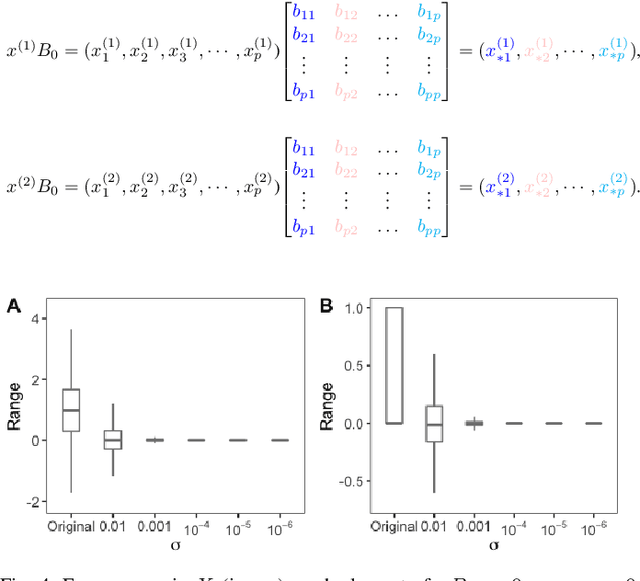
Scientific collaborations benefit from collaborative learning of distributed sources, but remain difficult to achieve when data are sensitive. In recent years, privacy preserving techniques have been widely studied to analyze distributed data across different agencies while protecting sensitive information. Secure multiparty computation has been widely studied for privacy protection with high privacy level but intense computation cost. There are also other security techniques sacrificing partial data utility to reduce disclosure risk. A major challenge is to balance data utility and disclosure risk while maintaining high computation efficiency. In this paper, matrix masking technique is applied to encrypt data such that the secure schemes are against malicious adversaries while achieving local differential privacy. The proposed schemes are designed for linear models and can be implemented for both vertical and horizontal partitioning scenarios. Moreover, cross validation is studied to prevent overfitting and select optimal parameters without additional communication cost. Simulation results present the efficiency of proposed schemes to analyze dataset with millions of records and high-dimensional data (n << p).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge