Leveraging Evolutionary Search to Discover Self-Adaptive and Self-Organizing Cellular Automata
Paper and Code
May 16, 2014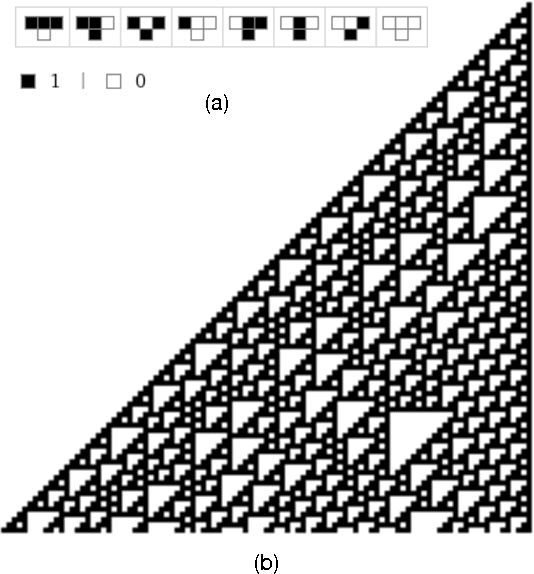

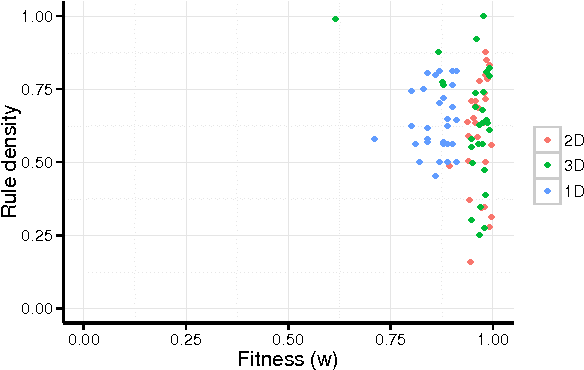

Building self-adaptive and self-organizing (SASO) systems is a challenging problem, in part because SASO principles are not yet well understood and few platforms exist for exploring them. Cellular automata (CA) are a well-studied approach to exploring the principles underlying self-organization. A CA comprises a lattice of cells whose states change over time based on a discrete update function. One challenge to developing CA is that the relationship of an update function, which describes the local behavior of each cell, to the global behavior of the entire CA is often unclear. As a result, many researchers have used stochastic search techniques, such as evolutionary algorithms, to automatically discover update functions that produce a desired global behavior. However, these update functions are typically defined in a way that does not provide for self-adaptation. Here we describe an approach to discovering CA update functions that are both self-adaptive and self-organizing. Specifically, we use a novel evolutionary algorithm-based approach to discover finite state machines (FSMs) that implement update functions for CA. We show how this approach is able to evolve FSM-based update functions that perform well on the density classification task for 1-, 2-, and 3-dimensional CA. Moreover, we show that these FSMs are self-adaptive, self-organizing, and highly scalable, often performing well on CA that are orders of magnitude larger than those used to evaluate performance during the evolutionary search. These results demonstrate that CA are a viable platform for studying the integration of self-adaptation and self-organization, and strengthen the case for using evolutionary algorithms as a component of SASO systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge