Legitimate against Illegitimate IRSs on MISO Wiretap Channels
Paper and Code
Mar 24, 2022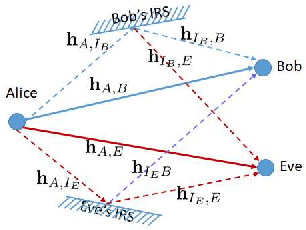
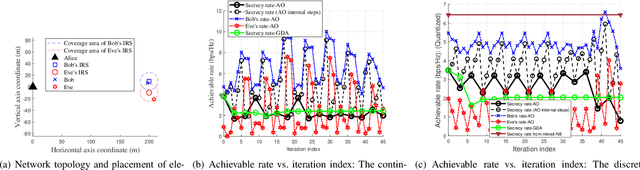
The low-cost legitimate intelligent reflecting surfaces (IRSs) are applied to the wiretap channel in physical layer security to enhance the secrecy rate. In practice, the eavesdropper can also deploy an IRS, namely illegitimate IRS, to deteriorate the secrecy rate. This paper studies the interplay between a transmitter, a legitimate IRS, and an illegitimate IRS in a multiple-input single-output (MISO) wiretap channel. We formulate a max-min secrecy rate problem, where all the information is available at the transmitter and the receivers. We aim to design an efficient transmit beamforming and phase shifting strategy of the legitimate IRS, under the worst-case secrecy rate achieved based on optimizing the phase-shifting strategy of the illegitimate IRS. We propose three solution methods based on the gradient descent ascent (GDA), the alternate optimization (AO), and the mixed Nash equilibrium (NE) in zero-sum games in strategic form. Simulation results show that for the continuous phase-shifting strategies, AO usually does not guarantee convergence, although it may achieve better performance than GDA in some iterations. GDA usually converges to a stationary point. Discrete phase-shifting strategies improve the convergence behavior of AO and GDA, while there is a single mixed NE with the highest secrecy rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge