Left-Invariant Diffusion on the Motion Group in terms of the Irreducible Representations of SO

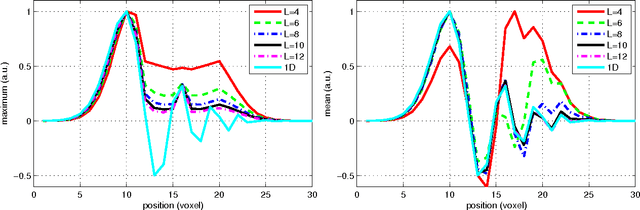
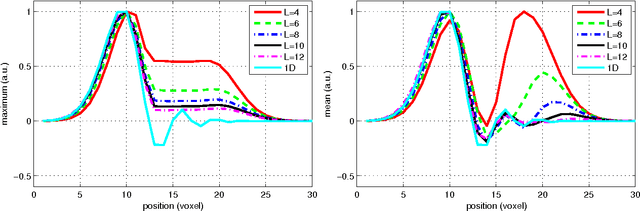
In this work we study the formulation of convection/diffusion equations on the 3D motion group SE(3) in terms of the irreducible representations of SO(3). Therefore, the left-invariant vector-fields on SE(3) are expressed as linear operators, that are differential forms in the translation coordinate and algebraic in the rotation. In the context of 3D image processing this approach avoids the explicit discretization of SO(3) or $S_2$, respectively. This is particular important for SO(3), where a direct discretization is infeasible due to the enormous memory consumption. We show two applications of the framework: one in the context of diffusion-weighted magnetic resonance imaging and one in the context of object detection.