Learning to Embed Probabilistic Structures Between Deterministic Chaos and Random Process in a Variational Bayes Predictive-Coding RNN

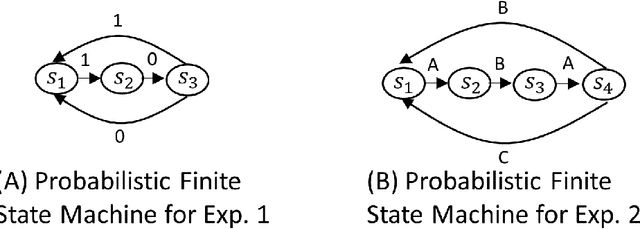
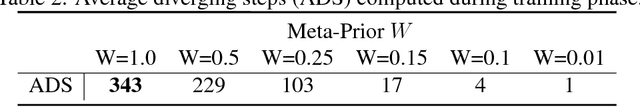
This study introduces a stochastic predictive-coding RNN model that can learn to extract probabilistic structures hidden in fluctuating temporal patterns by dynamically changing the uncertainty of latent variables. The learning process of the model involves maximizing the lower bound on the marginal likelihood of the sequential data, which consists of two terms. The first one is the expectation of prediction errors and the second one is the divergence of the prior and the approximated posterior. The main focus in the current study is to examine how weighting of the second term during learning affects the way of internally representing the uncertainty hidden in the sequence data. The simulation experiment on learning a simple probabilistic finite state machine demonstrates that the estimation of uncertainty in the latent variable approaches zero at each time step and that the network imitates the probabilistic structure of the target sequences by developing deterministic chaos in the case of the high weighting. On the contrary, in the case of the low weighting, the estimate of uncertainty increases significantly because of developing a random process in the network. The analysis shows that generalization in learning is most successful between these two extremes. Qualitatively, the same property has been observed in a trail of learning more complex sequence data consisting of probabilistic transitions between a set of hand-drawn primitive patterns using the model extended with hierarchy.