Learning Structured Gaussians to Approximate Deep Ensembles
Paper and Code
Mar 29, 2022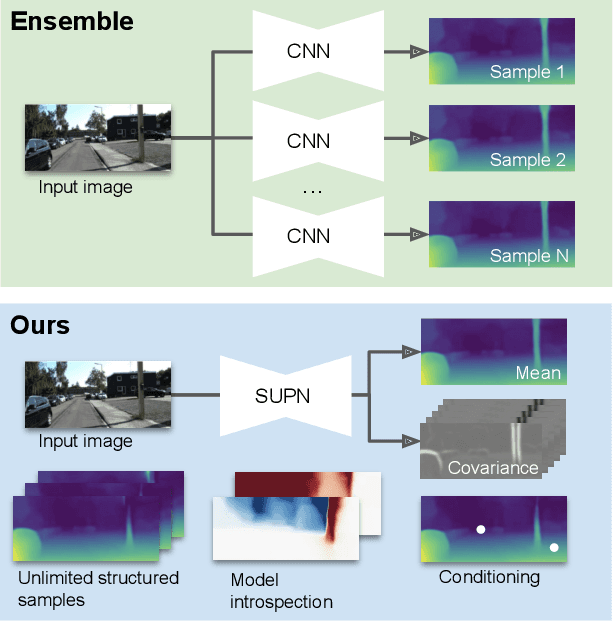

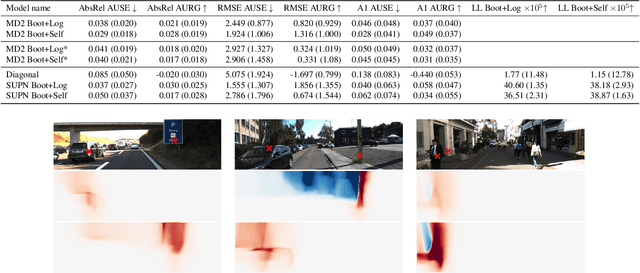
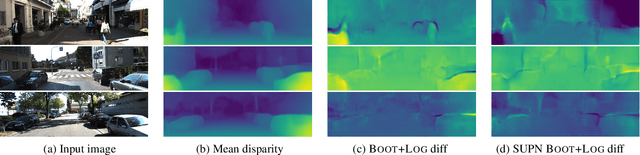
This paper proposes using a sparse-structured multivariate Gaussian to provide a closed-form approximator for the output of probabilistic ensemble models used for dense image prediction tasks. This is achieved through a convolutional neural network that predicts the mean and covariance of the distribution, where the inverse covariance is parameterised by a sparsely structured Cholesky matrix. Similarly to distillation approaches, our single network is trained to maximise the probability of samples from pre-trained probabilistic models, in this work we use a fixed ensemble of networks. Once trained, our compact representation can be used to efficiently draw spatially correlated samples from the approximated output distribution. Importantly, this approach captures the uncertainty and structured correlations in the predictions explicitly in a formal distribution, rather than implicitly through sampling alone. This allows direct introspection of the model, enabling visualisation of the learned structure. Moreover, this formulation provides two further benefits: estimation of a sample probability, and the introduction of arbitrary spatial conditioning at test time. We demonstrate the merits of our approach on monocular depth estimation and show that the advantages of our approach are obtained with comparable quantitative performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge