Learning Sampling Distributions for Model Predictive Control
Paper and Code
Dec 05, 2022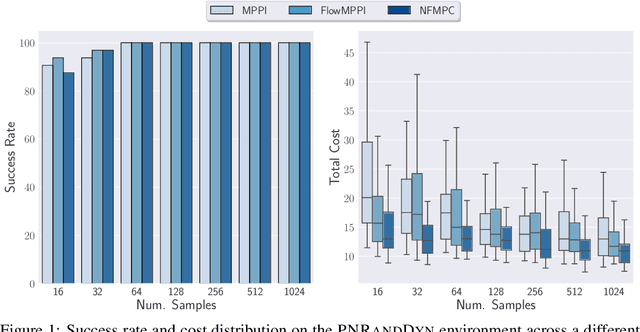
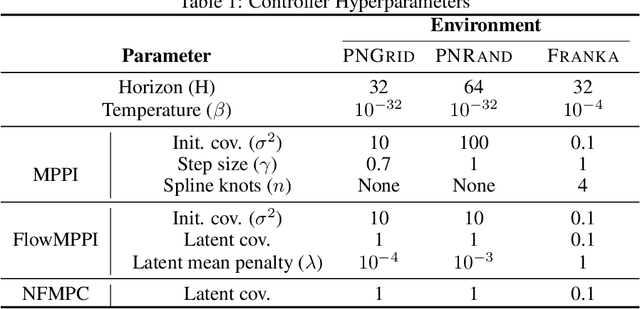

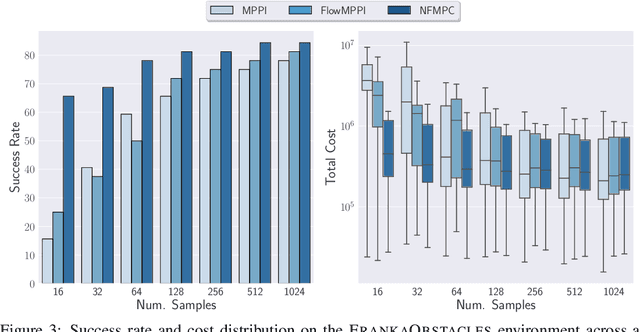
Sampling-based methods have become a cornerstone of contemporary approaches to Model Predictive Control (MPC), as they make no restrictions on the differentiability of the dynamics or cost function and are straightforward to parallelize. However, their efficacy is highly dependent on the quality of the sampling distribution itself, which is often assumed to be simple, like a Gaussian. This restriction can result in samples which are far from optimal, leading to poor performance. Recent work has explored improving the performance of MPC by sampling in a learned latent space of controls. However, these methods ultimately perform all MPC parameter updates and warm-starting between time steps in the control space. This requires us to rely on a number of heuristics for generating samples and updating the distribution and may lead to sub-optimal performance. Instead, we propose to carry out all operations in the latent space, allowing us to take full advantage of the learned distribution. Specifically, we frame the learning problem as bi-level optimization and show how to train the controller with backpropagation-through-time. By using a normalizing flow parameterization of the distribution, we can leverage its tractable density to avoid requiring differentiability of the dynamics and cost function. Finally, we evaluate the proposed approach on simulated robotics tasks and demonstrate its ability to surpass the performance of prior methods and scale better with a reduced number of samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge