Learning quantitative sequence-function relationships from massively parallel experiments
Paper and Code
Sep 22, 2015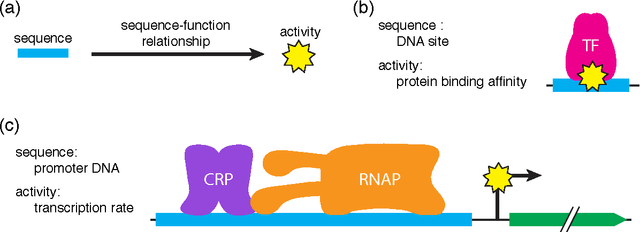
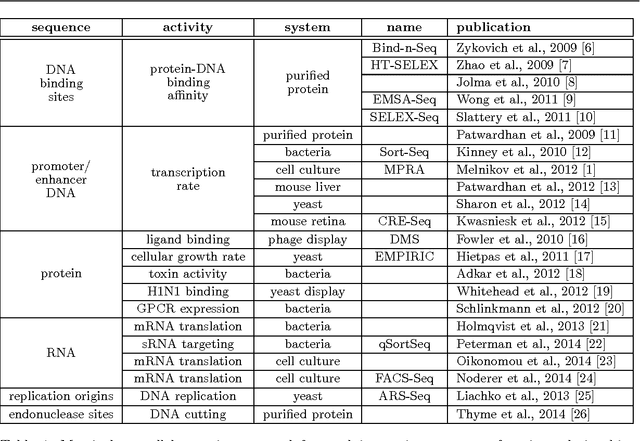
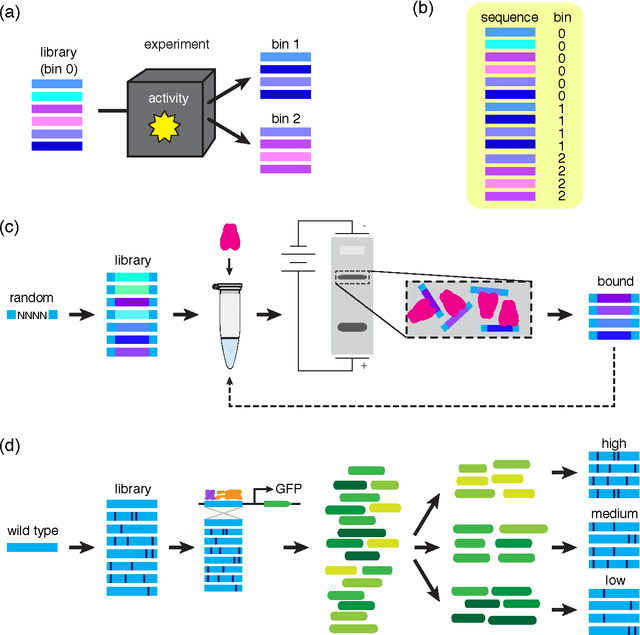
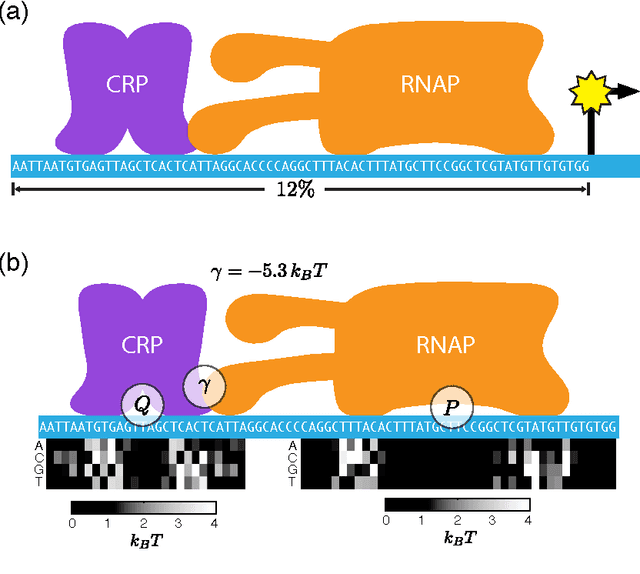
A fundamental aspect of biological information processing is the ubiquity of sequence-function relationships -- functions that map the sequence of DNA, RNA, or protein to a biochemically relevant activity. Most sequence-function relationships in biology are quantitative, but only recently have experimental techniques for effectively measuring these relationships been developed. The advent of such "massively parallel" experiments presents an exciting opportunity for the concepts and methods of statistical physics to inform the study of biological systems. After reviewing these recent experimental advances, we focus on the problem of how to infer parametric models of sequence-function relationships from the data produced by these experiments. Specifically, we retrace and extend recent theoretical work showing that inference based on mutual information, not the standard likelihood-based approach, is often necessary for accurately learning the parameters of these models. Closely connected with this result is the emergence of "diffeomorphic modes" -- directions in parameter space that are far less constrained by data than likelihood-based inference would suggest. Analogous to Goldstone modes in physics, diffeomorphic modes arise from an arbitrarily broken symmetry of the inference problem. An analytically tractable model of a massively parallel experiment is then described, providing an explicit demonstration of these fundamental aspects of statistical inference. This paper concludes with an outlook on the theoretical and computational challenges currently facing studies of quantitative sequence-function relationships.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge