Learning phylogenetic trees as hyperbolic point configurations
Paper and Code
Apr 23, 2021
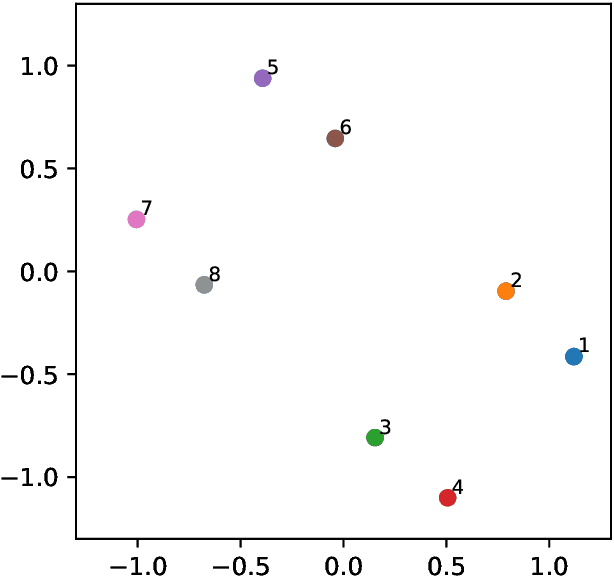
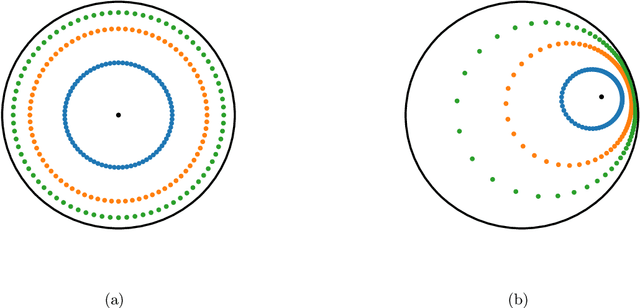
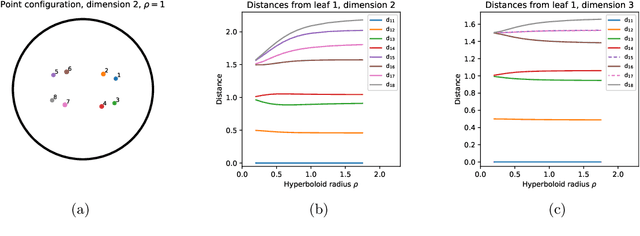
An alternative to independent pairwise distance estimation is proposed that uses hyperbolic geometry to jointly estimate pairwise distances subject to a weakening of the four point condition that characterises tree metrics. Specifically, taxa are represented as points in hyperbolic space such that the distance between a pair of points accounts for the site differences between the corresponding taxa. The proposed algorithm iteratively rearranges the points to increase an objective function that is shown empirically to increase the log-likelihood employed in tree search. Unlike the log-likelihood on tree space, the proposed objective function is differentiable, allowing for the use of gradient-based techniques in its optimisation. It is shown that the error term in the weakened four point condition is bounded by a linear function of the radius parameter of the hyperboloid model, which controls the curvature of the space. The error may thus be made as small as desired, within the bounds of computational precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge