Learning Numeracy: Binary Arithmetic with Neural Turing Machines

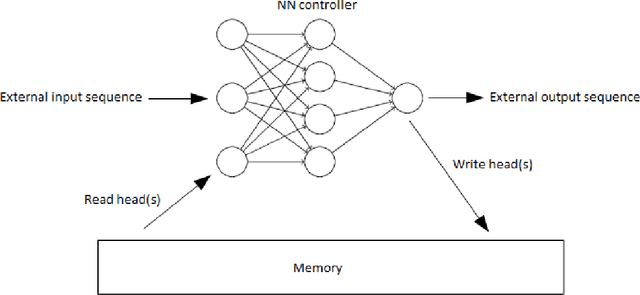
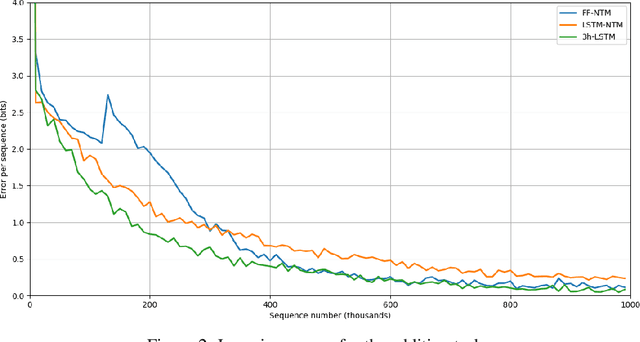
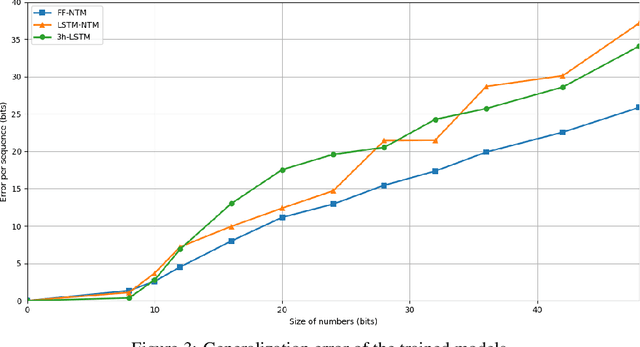
One of the main problems encountered so far with recurrent neural networks is that they struggle to retain long-time information dependencies in their recurrent connections. Neural Turing Machines (NTMs) attempt to mitigate this issue by providing the neural network with an external portion of memory, in which information can be stored and manipulated later on. The whole mechanism is differentiable end-to-end, allowing the network to learn how to utilise this long-term memory via SGD. This allows NTMs to infer simple algorithms directly from data sequences. Nonetheless, the model can be hard to train due to a large number of parameters and interacting components and little related work is present. In this work we use a NTM to learn and generalise two arithmetical tasks: binary addition and multiplication. These tasks are two fundamental algorithmic examples in computer science, and are a lot more challenging than the previously explored ones, with which we aim to shed some light on the capabilities on this neural model.