Learning-NUM: Network Utility Maximization with Unknown Utility Functions and Queueing Delay
Paper and Code
Dec 16, 2020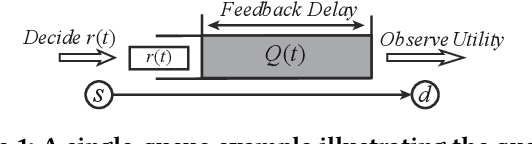
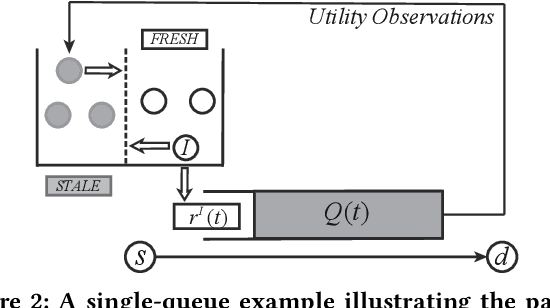
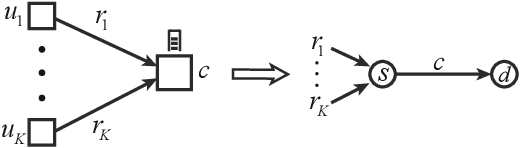

Network Utility Maximization (NUM) studies the problems of allocating traffic rates to network users in order to maximize the users' total utility subject to network resource constraints. In this paper, we propose a new NUM framework, Learning-NUM, where the users' utility functions are unknown apriori and the utility function values of the traffic rates can be observed only after the corresponding traffic is delivered to the destination, which means that the utility feedback experiences \textit{queueing delay}. The goal is to design a policy that gradually learns the utility functions and makes rate allocation and network scheduling/routing decisions so as to maximize the total utility obtained over a finite time horizon $T$. In addition to unknown utility functions and stochastic constraints, a central challenge of our problem lies in the queueing delay of the observations, which may be unbounded and depends on the decisions of the policy. We first show that the expected total utility obtained by the best dynamic policy is upper bounded by the solution to a static optimization problem. Without the presence of feedback delay, we design an algorithm based on the ideas of gradient estimation and Max-Weight scheduling. To handle the feedback delay, we embed the algorithm in a parallel-instance paradigm to form a policy that achieves $\tilde{O}(T^{3/4})$-regret, i.e., the difference between the expected utility obtained by the best dynamic policy and our policy is in $\tilde{O}(T^{3/4})$. Finally, to demonstrate the practical applicability of the Learning-NUM framework, we apply it to three application scenarios including database query, job scheduling and video streaming. We further conduct simulations on the job scheduling application to evaluate the empirical performance of our policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge