Learning Neural Networks under Input-Output Specifications
Paper and Code
Feb 23, 2022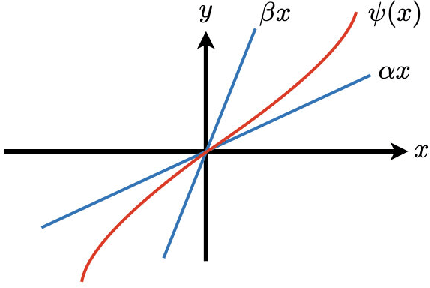
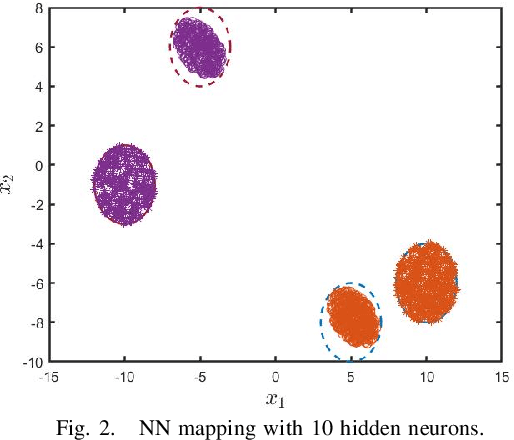
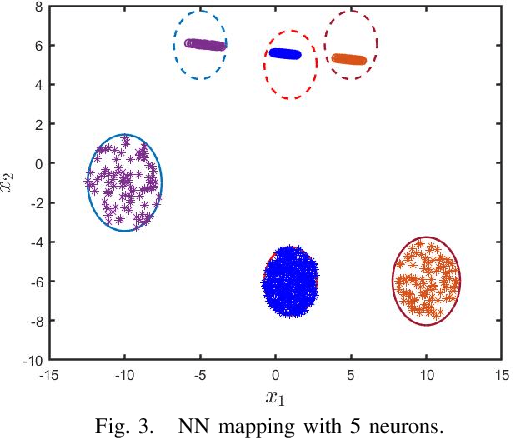
In this paper, we examine an important problem of learning neural networks that certifiably meet certain specifications on input-output behaviors. Our strategy is to find an inner approximation of the set of admissible policy parameters, which is convex in a transformed space. To this end, we address the key technical challenge of convexifying the verification condition for neural networks, which is derived by abstracting the nonlinear specifications and activation functions with quadratic constraints. In particular, we propose a reparametrization scheme of the original neural network based on loop transformation, which leads to a convex condition that can be enforced during learning. This theoretical construction is validated in an experiment that specifies reachable sets for different regions of inputs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge