Learning Neural Networks on SVD Boosted Latent Spaces for Semantic Classification
Paper and Code
Jan 03, 2021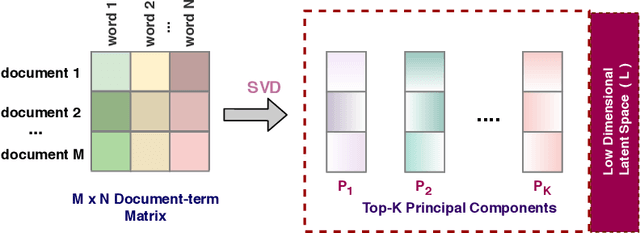
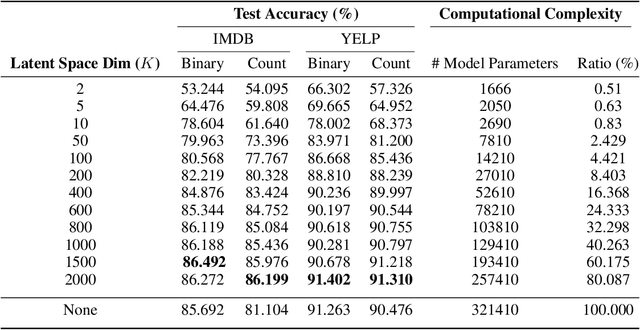
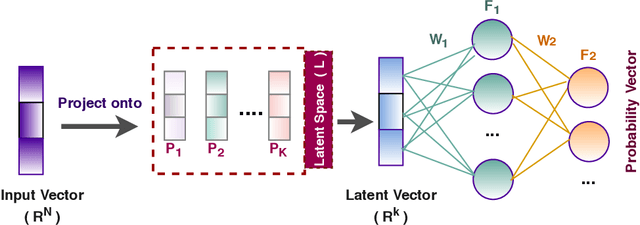
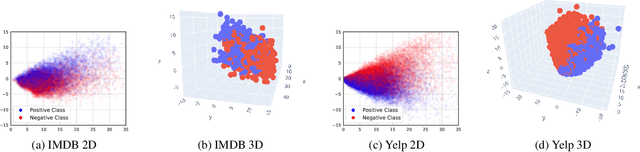
The availability of large amounts of data and compelling computation power have made deep learning models much popular for text classification and sentiment analysis. Deep neural networks have achieved competitive performance on the above tasks when trained on naive text representations such as word count, term frequency, and binary matrix embeddings. However, many of the above representations result in the input space having a dimension of the order of the vocabulary size, which is enormous. This leads to a blow-up in the number of parameters to be learned, and the computational cost becomes infeasible when scaling to domains that require retaining a colossal vocabulary. This work proposes using singular value decomposition to transform the high dimensional input space to a lower-dimensional latent space. We show that neural networks trained on this lower-dimensional space are not only able to retain performance while savoring significant reduction in the computational complexity but, in many situations, also outperforms the classical neural networks trained on the native input space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge