Learning Memory Kernels in Generalized Langevin Equations

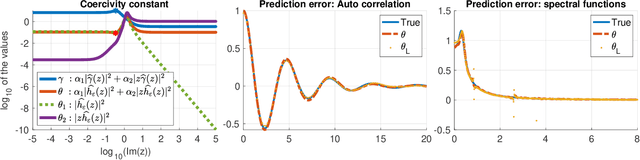
We introduce a novel approach for learning memory kernels in Generalized Langevin Equations. This approach initially utilizes a regularized Prony method to estimate correlation functions from trajectory data, followed by regression over a Sobolev norm-based loss function with RKHS regularization. Our approach guarantees improved performance within an exponentially weighted $L^2$ space, with the kernel estimation error controlled by the error in estimated correlation functions. We demonstrate the superiority of our estimator compared to other regression estimators that rely on $L^2$ loss functions and also an estimator derived from the inverse Laplace transform, using numerical examples that highlight its consistent advantage across various weight parameter selections. Additionally, we provide examples that include the application of force and drift terms in the equation.