Learning loopy graphical models with latent variables: Efficient methods and guarantees
Paper and Code
Apr 22, 2013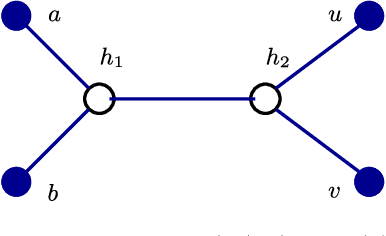
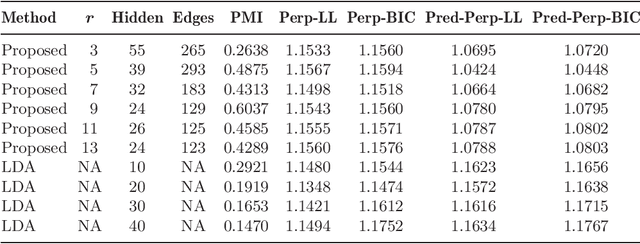
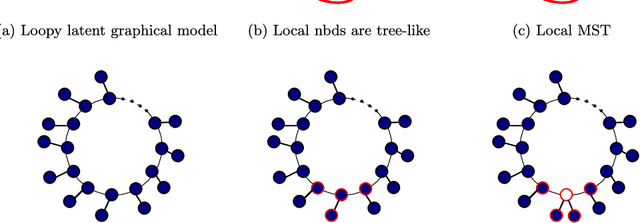

The problem of structure estimation in graphical models with latent variables is considered. We characterize conditions for tractable graph estimation and develop efficient methods with provable guarantees. We consider models where the underlying Markov graph is locally tree-like, and the model is in the regime of correlation decay. For the special case of the Ising model, the number of samples $n$ required for structural consistency of our method scales as $n=\Omega(\theta_{\min}^{-\delta\eta(\eta+1)-2}\log p)$, where p is the number of variables, $\theta_{\min}$ is the minimum edge potential, $\delta$ is the depth (i.e., distance from a hidden node to the nearest observed nodes), and $\eta$ is a parameter which depends on the bounds on node and edge potentials in the Ising model. Necessary conditions for structural consistency under any algorithm are derived and our method nearly matches the lower bound on sample requirements. Further, the proposed method is practical to implement and provides flexibility to control the number of latent variables and the cycle lengths in the output graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge