Learning interaction kernels in mean-field equations of 1st-order systems of interacting particles
Paper and Code
Oct 29, 2020
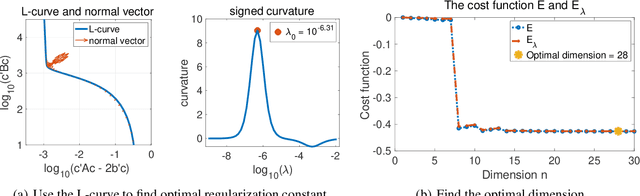

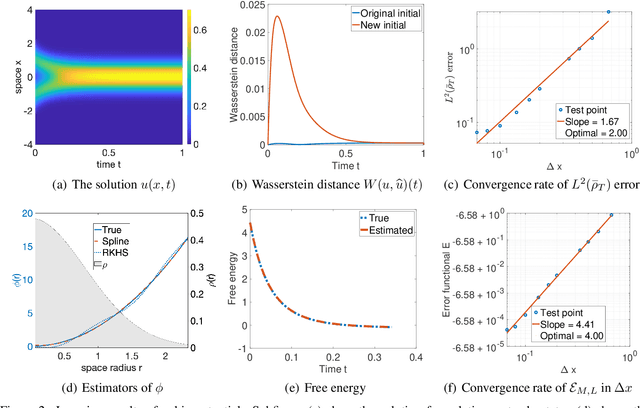
We introduce a nonparametric algorithm to learn interaction kernels of mean-field equations for 1st-order systems of interacting particles. The data consist of discrete space-time observations of the solution. By least squares with regularization, the algorithm learns the kernel on data-adaptive hypothesis spaces efficiently. A key ingredient is a probabilistic error functional derived from the likelihood of the mean-field equation's diffusion process. The estimator converges, in a reproducing kernel Hilbert space and an L2 space under an identifiability condition, at a rate optimal in the sense that it equals the numerical integrator's order. We demonstrate our algorithm on three typical examples: the opinion dynamics with a piecewise linear kernel, the granular media model with a quadratic kernel, and the aggregation-diffusion with a repulsive-attractive kernel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge