Learning Embedding of 3D models with Quadric Loss
Paper and Code
Jul 24, 2019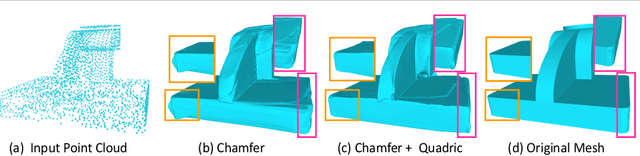
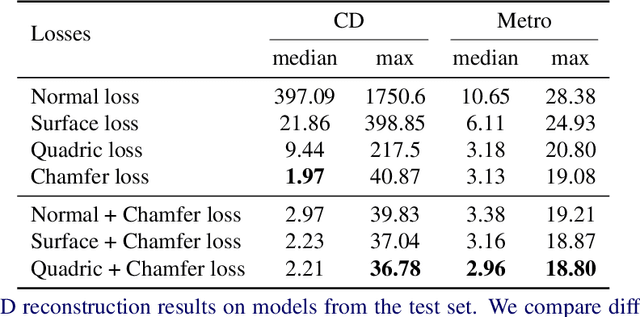
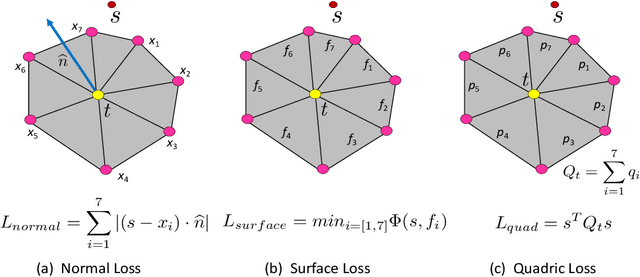
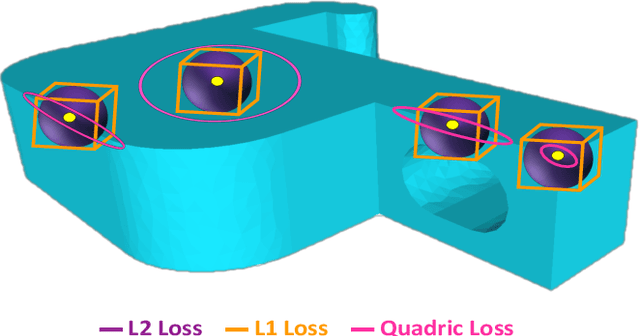
Sharp features such as edges and corners play an important role in the perception of 3D models. In order to capture them better, we propose quadric loss, a point-surface loss function, which minimizes the quadric error between the reconstructed points and the input surface. Computation of Quadric loss is easy, efficient since the quadric matrices can be computed apriori, and is fully differentiable, making quadric loss suitable for training point and mesh based architectures. Through extensive experiments we show the merits and demerits of quadric loss. When combined with Chamfer loss, quadric loss achieves better reconstruction results as compared to any one of them or other point-surface loss functions.
* Accepted to BMVC 2019 for Oral Presentation
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge