Learning Covariant Feature Detectors
Paper and Code
Sep 09, 2016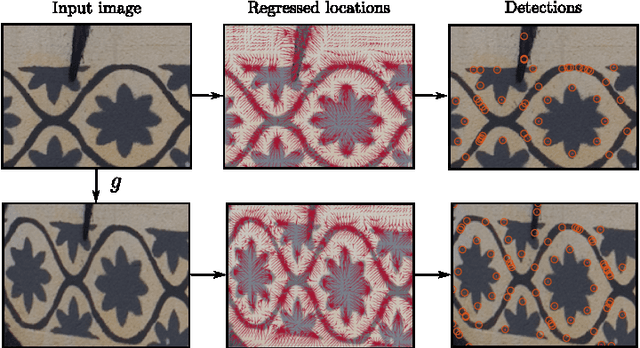



Local covariant feature detection, namely the problem of extracting viewpoint invariant features from images, has so far largely resisted the application of machine learning techniques. In this paper, we propose the first fully general formulation for learning local covariant feature detectors. We propose to cast detection as a regression problem, enabling the use of powerful regressors such as deep neural networks. We then derive a covariance constraint that can be used to automatically learn which visual structures provide stable anchors for local feature detection. We support these ideas theoretically, proposing a novel analysis of local features in term of geometric transformations, and we show that all common and many uncommon detectors can be derived in this framework. Finally, we present empirical results on translation and rotation covariant detectors on standard feature benchmarks, showing the power and flexibility of the framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge