Layerwise Bregman Representation Learning with Applications to Knowledge Distillation
Paper and Code
Sep 15, 2022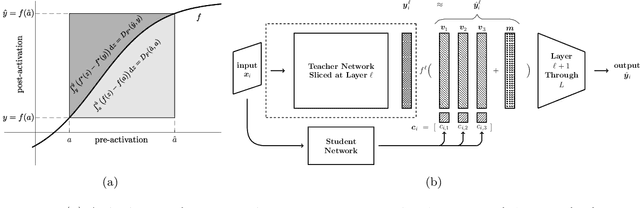
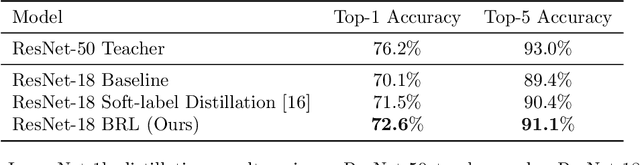
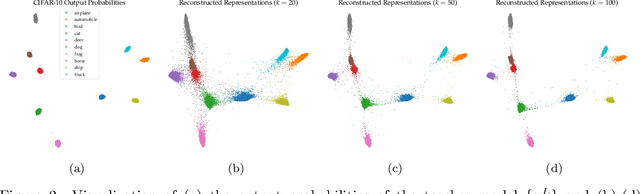
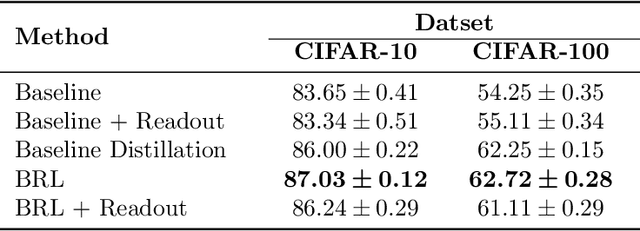
In this work, we propose a novel approach for layerwise representation learning of a trained neural network. In particular, we form a Bregman divergence based on the layer's transfer function and construct an extension of the original Bregman PCA formulation by incorporating a mean vector and normalizing the principal directions with respect to the geometry of the local convex function around the mean. This generalization allows exporting the learned representation as a fixed layer with a non-linearity. As an application to knowledge distillation, we cast the learning problem for the student network as predicting the compression coefficients of the teacher's representations, which are passed as the input to the imported layer. Our empirical findings indicate that our approach is substantially more effective for transferring information between networks than typical teacher-student training using the teacher's penultimate layer representations and soft labels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge