Last iterate convergence of SGD for Least-Squares in the Interpolation regime
Paper and Code
Feb 05, 2021
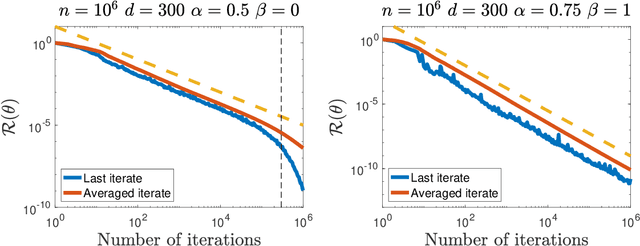


Motivated by the recent successes of neural networks that have the ability to fit the data perfectly and generalize well, we study the noiseless model in the fundamental least-squares setup. We assume that an optimum predictor fits perfectly inputs and outputs $\langle \theta_* , \phi(X) \rangle = Y$, where $\phi(X)$ stands for a possibly infinite dimensional non-linear feature map. To solve this problem, we consider the estimator given by the last iterate of stochastic gradient descent (SGD) with constant step-size. In this context, our contribution is two fold: (i) from a (stochastic) optimization perspective, we exhibit an archetypal problem where we can show explicitly the convergence of SGD final iterate for a non-strongly convex problem with constant step-size whereas usual results use some form of average and (ii) from a statistical perspective, we give explicit non-asymptotic convergence rates in the over-parameterized setting and leverage a fine-grained parameterization of the problem to exhibit polynomial rates that can be faster than $O(1/T)$. The link with reproducing kernel Hilbert spaces is established.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge